(a)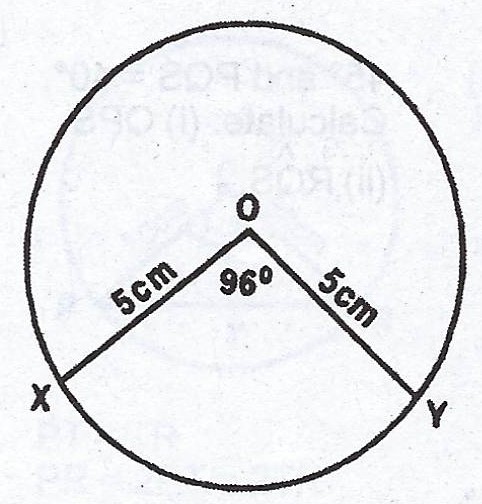 
In the diagram, XY is a chord of a circle of radius 5cm. The chord subtends an angle 96° at the centre. Calculate, correct to three significant figures, the area of the minor segment cut-off. (Take \(\pi = \frac{22}{7}\)).
(b)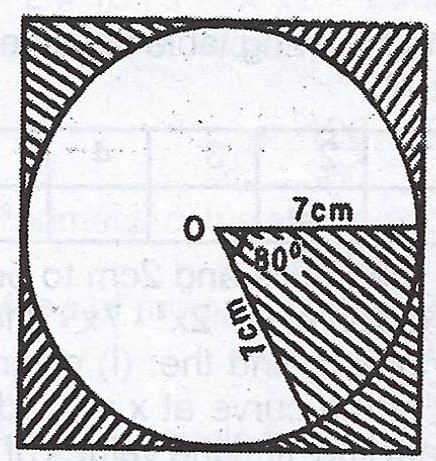 
The figure shows a circle inscribed in a square. If a portion of the circle is shaded with some portions of the square, calculate the total area of the shaded portions. [Take \(\pi = \frac{22}{7}\)].
Explanation
(a) Area of minor sector = \(\frac{\theta}{360} \times \pi r^{2}\)
= \(\frac{96}{360} \times \frac{22}{7} \times 5^{2}\)
= \(20.95 cm^{2}\)
Area of triangle formed from the sector = \(\frac{1}{2} r^{2} \sin \theta\)
= \(\frac{1}{2} \times 5^{2} \times \sin 96\)
= \(12.43 cm^{2}\)
\(\therefore \text{The area of minor segment} = 20.95 - 12.43\)
= \(8.52 cm^{2}\)
(b) Area of minor sector = \(\frac{\theta}{360} \times \pi r^{2}\)
= \(\frac{80}{360} \times \frac{22}{7} \times 7^{2}\)
= \(34.22 cm^{2}\)
Area of the square = \((14)^{2} = 196 cm^{2}\)
Area of the circle = \(\pi r^{2} = \frac{22}{7} \times 7^{2} = 154 cm^{2}\)
Area of the shaded portion in the square = \(196 - 154 = 42 cm^{2}\)
Total area of the shaded portions = \(42 + 34.22\)
= \(76.22 cm^{2} \approxeq 76.2 cm^{2}\)