(a) Simplify : \(\sqrt{1001_{two}}\), leaving your answer in base two.
(b) 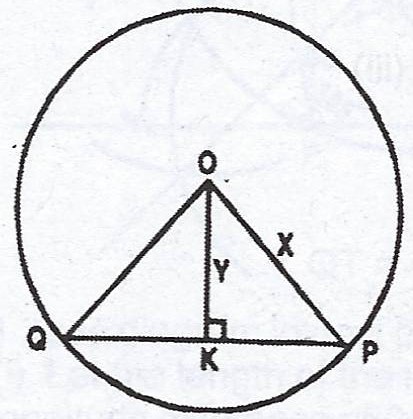
In the diagram, O is the centre of the circle radius x. /PQ/ = z, /OK/ = y and < OKP = 90°. Find the value of z in terms of x and y.
(c) 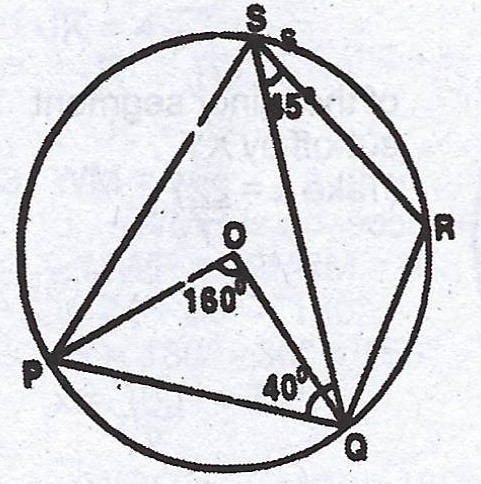
In the diagram, P, Q, R and S are points of the circle centre O. \(\stackrel\frown{POQ} = 160°\), \(\stackrel\frown{QSR} = 45°\) and \(\stackrel\frown{PQS} = 40°\). Calculate, (i) < QPS ; (ii) < RQS.
Explanation
(a) \(1001_{2} = 1 \times 2^{3} + 0 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0}\)
= \(8 + 0 + 0 + 1\)
= 9
\(\sqrt{9} = 3_{10}\)
| 2 | 3 |
| 2 | 1 r 1 |
| 0 r 1 |
\(\therefore \sqrt{1001_{2}} = 11_{2}\)
(b) In \(\Delta QOP, OQ = OP\)
\(\therefore QK = KP\)
\(\Delta QOK = \Delta POK\) (right- angled triangle)
In \(\Delta POK\),
\(OP^{2} = PK^{2} + OK^{2}\)
\(x^{2} = y^{2} + (\frac{z}{2})^{2}\)
\(\frac{z^{2}}{4} = x^{2} - y^{2}\)
\(z^{2} = 4x^{2} - 4y^{2}\)
\(z = \sqrt{4(x^{2} - y^{2})}\)
\(z = 2\sqrt{x^{2} - y^{2}}\)
(c)(i) \(< PSQ = \frac{1}{2}(< POQ) = \frac{1}{2}(160°)\)
= 80°
In \(\Delta PSQ\),
\(< PQS + < QPS + < PSQ = 180°\)
\(40° + < QPS + 80° = 180°\)
\(< QPS = 180° - 120° = 60°\)
(ii) \(< PSR = < PSQ + < QSR\)
= \(80° + 45°\)
= \(125°\)
\(< PQS = < PQO + < RQS \)
= \(40° + < RQS\)
\(< PSR + < PQS = 180°\)
\(\therefore 125° + 40° + < RQS = 180°\)
\(< RQS = 180° - 165°\)
= \(15°\)

