(a) Copy and complete the table.
\(y = x^{2} – 2x – 2\) for \(-4 \leq x \leq 4\)
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 22 | -2 | 1 | 6 |
(b) Using a scale of 2 cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of \(y = x^{2} – 2x – 2\).
(c) Use your graph to find : (i) the roots of the equation \(x^{2} – 2x – 2 = 0\) ; (ii) the values of x for which \(x^{2} – 2x – 4\frac{1}{2} = 0\) ; (iii) the equation of the line of symmetry of the curve.
(a)  In the diagram, \(\Delta\) ABD is right-angled at B. |AB| = 3 cm, |AD| = 5 cm, \(\stackrel\frown{ACB}\) = 61° and \(\stackrel\frown{DAC}\) = x°. Calculate, correct to one decimal place, the value of x.
In the diagram, \(\Delta\) ABD is right-angled at B. |AB| = 3 cm, |AD| = 5 cm, \(\stackrel\frown{ACB}\) = 61° and \(\stackrel\frown{DAC}\) = x°. Calculate, correct to one decimal place, the value of x.
(b)  In the diagram, OABCD is a pyramid with a square base of side 2cm and a slant height of 4 cm. Calculate, correct to three significant figures : (i) the vertical height of the pyramid ; (ii) the volume of the pyramid.
In the diagram, OABCD is a pyramid with a square base of side 2cm and a slant height of 4 cm. Calculate, correct to three significant figures : (i) the vertical height of the pyramid ; (ii) the volume of the pyramid.
The table shows the age distributions of the members of a club.
| Age (years) | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 |
| Frequency | 7 | 18 | 25 | 17 | 9 | 4 |
(a) Calculate, correct to one decimal place, the mean age.
(b) (i) Draw a histogram to illustrate the information.
(ii) Use the histogram to estimate the modal age .
(c) If a member is selected at random, what is the probability that he/she is in the modal class?
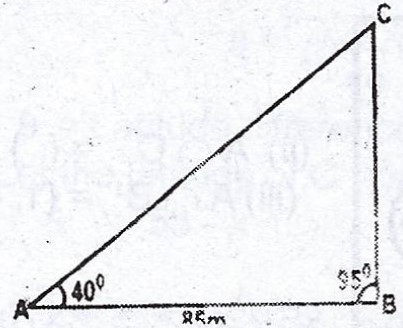
The sketch shows a plot of land .
(a) Using a scale of 1 cm to 10m, draw an accurate diagram of the plot ;
(b) Construct : (i) The locus \(l_{1}\) of points equidistant from AC and BC ; (ii) the locus \(l_{2}\) of points 60m from A.
(c) A tree T inside the plot is on both \(l_{1}\) and \(l_{2}\). Locate T and find |TC| in metres.
(d) A flagpole, P is to be placed such that it it is nearer AC than BC and more than 60m from A. Shade the regions where P can be located.
(a) Find the smallest integer that satisfies the inequality \(x + 8 < 4x – 15\).
(b) A sales girl is paid a monthly salary of N2,500 in addition to a commission of 5 kobo in the naira on all sales made by her during the month. If her sales for a month amounts to N200,000.00, calculate her income for that month.
(c) 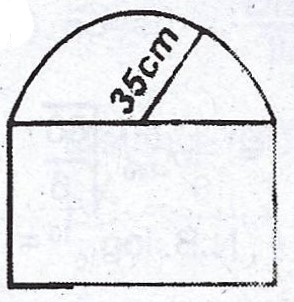 The diagram shows a window consisting of a rectangular and semi- circular parts. The radius of the semi- circular part is 35 cm and the height of the rectangular part is 50 cm. Find the area of the window. [Take \(\pi = \frac{22}{7}\)].
The diagram shows a window consisting of a rectangular and semi- circular parts. The radius of the semi- circular part is 35 cm and the height of the rectangular part is 50 cm. Find the area of the window. [Take \(\pi = \frac{22}{7}\)].
(a) A plane flies due East from A(lat. 53°N, long. 25°E) to a point B(lat. 53°N, long. 85°E) at an average speed of 400 km/h. The plane then flies South from B to a point C 2000km away. Calculate, correct to the nearest whole number :
(a) the distance between A and B.
(b) the time the plane takes to reach point B ;
(c) the latitude of C.
[Take radius of the earth = 6400km; \(\pi = \frac{22}{7}\)].
(a) A regular polygon of n sides is such that each interior angle is 120° greater than the exterior angle. Find :
(i) the value of n ; (ii) the sum of all the interior angles.
(b) A boy walks 6km from a point P to a point Q on a bearing of 065°. He then walks to a point R, a distance of 13km, on a bearing of 146°.
(i) Sketch the diagram of his movement. (ii) Calculate, correct to the nearest kilometre, the distance PR.
(a) Without using mathematical table or calculator, evaluate : \(\sqrt{\frac{0.18 \times 12.5}{0.05 \times 0.2}}\).
(b) Simplify : \(\frac{8 – 4\sqrt{18}}{\sqrt{50}}\).
(c) x, y and z are related such that x varies directly as the cube of y and inversely as the square of z. If x = 108 when y = 3 and z = 4, find z when x = 4000 and y = 10.
(a) 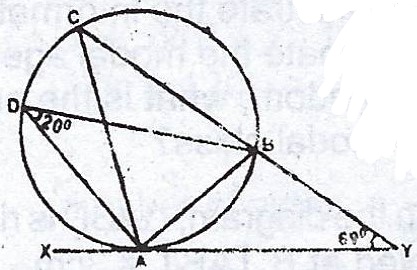
In the diagram, A, B, C and D are points on the circumference of a circle. XY is a tangent at A. Find : (i) < CAX ; (ii) < ABY.
(b) If (m + 1) and (m – 3) are factors of \(m^{2} – km + c\), find the values of k and c.
(a) Two fair die are thrown once. Find the probabitlity of getting : (i) the same digit ; (ii) a total score greater than 5.
(b) Given that \(x = \cos 30°\) and \(y = \sin 30°\), evaluate without using a mathematical table or calculator : \(\frac{x^{2} + y^{2}}{y^{2} – x^{2}}\).
(a) Simplify : \(\frac{5}{8} of 2\frac{1}{2} – \frac{3}{4} \div \frac{3}{5}\).
(b) A cone and a right pyramid have equal heights and volumes. If the area of the base of the pyramid is \(154 cm^{2}\), find the base radius of the cone. [Take \(\pi = \frac{22}{7}\)].
(a) Evaluate : \(2 \div (\frac{64}{125})^{-\frac{2}{3}}\)
(b) The lines \(y = 3x + 5\) and \(y = – 4x – 1\) intersect at a point k. Find the coordinates of k.
(a) Evaluate without using the mathematical table or calculator, \(\log_{10} \sqrt{30} – \log_{10} \sqrt{6} + \log_{10} \sqrt{2}\).
(b) 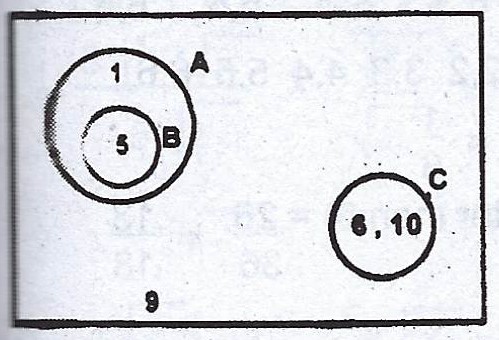
\(U = {1, 2, 3, …, 10} ; A = {1, 2, 3, 4, 5} ; B = {2, 3, 5}\) and \(C = {6, 8, 10}\). (i) Given that the Venn diagram represents the sets above, copy and fill in the elements.
(ii) Find \(A \cap C\) ; (iii) Find \(A \cap B’\).
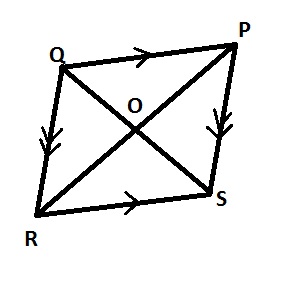
The figure shows a quadrilateral PQRS having equal sides and opposite sides parallel. The diagonals PR and QS intersect perpendicularly at O, Which of the following statements cannot be correct
- A. |PO|=|RO|
- B. PQR is an equilateral triangle
- C. PQRX is a parallelogram
- D. There are two lines of symmetry
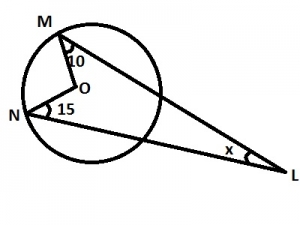
In the diagram, O is the center of the circle, ∠MON = 80o, ∠LMO = 10o and ∠LNO = 15o. Calculate the value of x
- A. 40o
- B. 50o
- C. 55o
- D. 75o
The monthly salary of a man increased from N2,700 to N3,200. Find the percentage increase
- A. 10%
- B. 15%
- C. 15.6%
- D. 18.5%
Ladi sold a car for N84,000 at a loss of 4%. How much did ladi buy the car?
- A. 80,500
- B. 80,640
- C. 87,360
- D. 87,500
If \(y \alpha x\(^{\frac{1}{2}}\) and \(y = 1\frac{1}{4}\) when x = 4, find the value of y when \(x = \frac{1}{2}\)
- A. \(2\frac{1}{2}\)
- B. 5
- C. 10
- D. 80
A rectangular packet has inner dimension 16cm by 12cm by 6cm. How many cubes of sugar of side 2cm can be neatly packed into the packet?
- A. 90
- B. 144
- C. 150
- D. 288
XOY is a real sector of a circle center O of radius 3.5cm which subtends an angle of 144o at the center. Calculate, in term of \(\pi\), the area of the sector
- A. 1.4\(\pi\)cm2
- B. 2.8\(\pi\)cm2
- C. 4.9\(\pi\)cm2
- D. 9.8\(\pi\)cm2
The angle of elevation of the top of a cliff 15 meters high from a landmark is 60º. How far is the landmark from the foot of the cliff? Leave your answer in surd form
- A. \(15\sqrt{3}m\)
- B. \(15\sqrt{2}m\)
- C. \(10\sqrt{3}m\)
- D. \(5\sqrt{3}m\)


