(a) Evaluate without using the mathematical table or calculator, \(\log_{10} \sqrt{30} – \log_{10} \sqrt{6} + \log_{10} \sqrt{2}\).
(b) 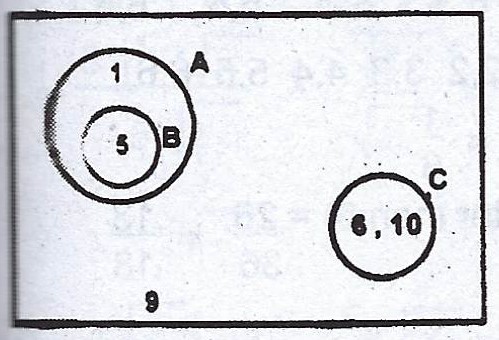
\(U = {1, 2, 3, …, 10} ; A = {1, 2, 3, 4, 5} ; B = {2, 3, 5}\) and \(C = {6, 8, 10}\). (i) Given that the Venn diagram represents the sets above, copy and fill in the elements.
(ii) Find \(A \cap C\) ; (iii) Find \(A \cap B’\).
Explanation
(a) \(\log_{10} \sqrt{30} - \log_{10} \sqrt{6} + \log_{10} \sqrt{2}\)
= \(\log_{10} (\sqrt{\frac{30}{6}} \times \sqrt{2})\)
= \(\log_{10} (\sqrt{5} \times \sqrt{2})\)
= \(\log_{10} \sqrt{10}\)
= \(\log_{10} (10^{\frac{1}{2}})\)
= \(\frac{1}{2} \log_{10} 10\)
= \(\frac{1}{2}\).
(b) 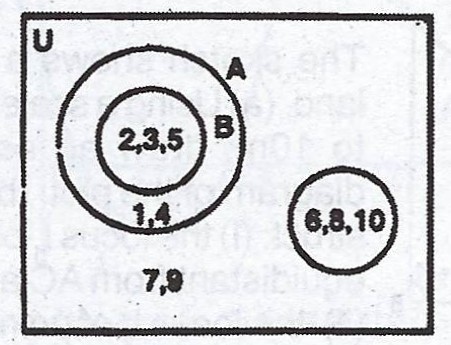
(ii) \(A \cap C = { } \)
(iii) \(A \cap B' = {1, 4}\).

