(a) 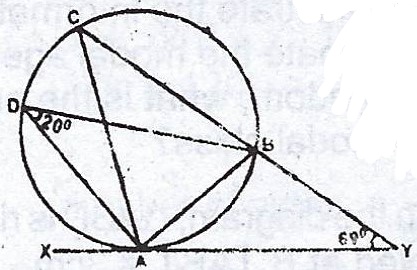
In the diagram, A, B, C and D are points on the circumference of a circle. XY is a tangent at A. Find : (i) < CAX ; (ii) < ABY.
(b) If (m + 1) and (m – 3) are factors of \(m^{2} – km + c\), find the values of k and c.
Explanation
(a) \(< ADB = < ACB = 20°\) (Angle in the same segment).
In \(\Delta ACY\),
\(\hat{C} = < ACB\)
(i) \(\hat{C} + \hat{A} + \hat{Y} = 180°\)
\(20° + \hat{A} + 60° = 180°\)
\(\hat{A} = 180° - 80° = 100°\)
\(< CAY = \hat{A} = 100°\)
\(< CAX = 180° - 100° = 80°\)
(ii) In \(\Delta ACB\),
\(\hat{B} = \hat{C} = \frac{180° - 20°}{2} \)
= \(\frac{160°}{2}\)
= \(80°\)
In \(\Delta ABY\),
\(< ABY = \hat{B} = 180° - 80°\)
= \(100°\)
(b) \((m + 1)(m - 3) \equiv m^{2} - km + c\)
\(m^{2} - 3m + m - 3 = m^{2} - 2m - 3\)
\(m^{2} - 2m - 3 \equiv m^{2} - km + c\)
\(\implies k = 2 ; c = -3\)

