(a) A regular polygon of n sides is such that each interior angle is 120° greater than the exterior angle. Find :
(i) the value of n ; (ii) the sum of all the interior angles.
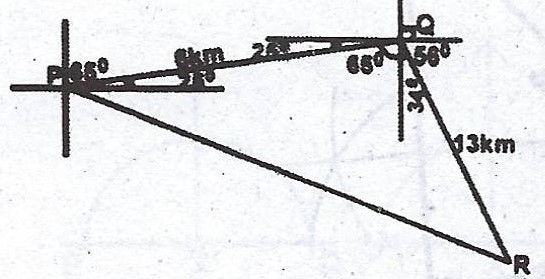
(b) A boy walks 6km from a point P to a point Q on a bearing of 065°. He then walks to a point R, a distance of 13km, on a bearing of 146°.
(i) Sketch the diagram of his movement. (ii) Calculate, correct to the nearest kilometre, the distance PR.
Explanation
(a) (i) Let the exterior angle be x
Let the interior angle be x + 120°.
Exterior angle + Interior angle = 180°
\(\therefore x + x + 120 = 180 \implies 2x + 120 = 180\)
\(2x = 60 \implies x = 30°\)
Number of sides = \(\frac{360}{\text{exterior angle}}\)
= \(\frac{360}{30} = 12 sides\)
(ii) Sum of interior angle = \((2n - 4) \times 90°\)
= \((2(12) - 4) \times 90°\)
= \(20 \times 90\)
= \(1800°\)
(b) Note : < PQR = 65° + 34° = 99°\)
\(|PR|^{2} = |PQ|^{2} + |QR|^{2} - 2(|QR|)(|PQ|) \cos 99\)
\(|PR|^{2} = 6^{2} + 13^{2} - 2(6)(13) \cos 99\)
\(|PR|^{2} = 205 - 156 \cos 99\)
\(|PR|^{2} = 205 + 24.40 = 229.40\)
\(|PR| = \sqrt{229.40}\)
= \(15.146 km\)
\(\approxeq 15 km\)

