(a) A plane flies due East from A(lat. 53°N, long. 25°E) to a point B(lat. 53°N, long. 85°E) at an average speed of 400 km/h. The plane then flies South from B to a point C 2000km away. Calculate, correct to the nearest whole number :
(a) the distance between A and B.
(b) the time the plane takes to reach point B ;
(c) the latitude of C.
[Take radius of the earth = 6400km; \(\pi = \frac{22}{7}\)].
Explanation
(a) 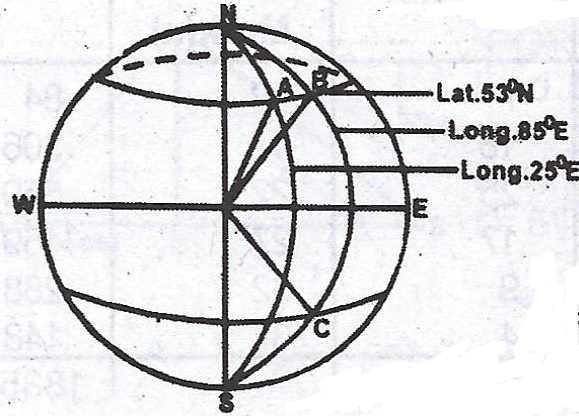
Longitude difference = 85° - 25° = 60°.
Distance AB along the parallel of latitude = \(\frac{\theta}{360°} \times 2\pi R \cos \alpha\)
\(AB = \frac{60}{360} \times 2 \times \frac{22}{7} \times 6400 \cos 53\)
= \(\frac{1}{6} \times \frac{44}{7} \times 3851.62\)
= \(4,035.03 km\)
\(\approxeq 4035 km\)
(b) \(Speed = \frac{Distance}{Time}\)
\(\therefore Time = \frac{Distance}{Speed}\)
= \(\frac{4035}{400}\)
\(\approxeq 10 hours\).
(c) Distance BC measured along the meridian
\(BC = \frac{\theta}{360} \times 2 \pi R\)
\(2000 = \frac{\theta}{360} \times 2 \times \frac{22}{7} \times 6400\)
\(\theta = 17.898° \approxeq 18°\)
\(\theta\) = Latitude difference
Let the latitude of C = x.
\(\theta = 53 - x\)
\(18 = 53 - x\)
\(x = 35°\)

