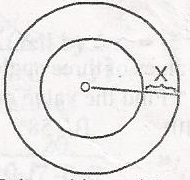
In the diagram, the two circles have a common centre O. If the area of the larger circle is 100\(\pi\) and that of the smaller circle is 49\(\pi\), find x
The correct answer is: B
Explanation
area of larger circle = 100\(\pi\)\(\pi r^2 = 100\pi\)
R2 = 100
R = 10(Radius)
Area of smaller circle = \(49 \pi\)
\(\pi r^2 = 49\pi\)
r2 = 49
r = 7(radius)
Since R = x + r
x = R - r
x = 10 - 7 = 3


