(a) A sector of a circle of radius 8cm subtends an angle of 90° at the centre of the circle. If the sector is folded without overlap to form the curved surface of a cone, find the :
(i) base radius ; (ii) height ; (iii) volume of the cone. [Take \(\pi = \frac{22}{7}\)].
(b) A map is drawn to a scale of 1 : 20,000. Use it to calculate the : (i) distance, in kilometres, represented by 4.5 cm on the map ;
Explanation
(a) (i) Length of sector = \(\frac{\theta}{360} \times 2\pi R\)
Length of the base of the cone formed = \(2\pi r\)
\(\frac{90}{360} \times 2 \times \pi \times 8 = 2\pi r\)
\(4\pi = 2\pi r\)
\(2r = 4 \implies r = 2 cm\)
The base radius of the cone = 2 cm.
(ii) Height of the cone
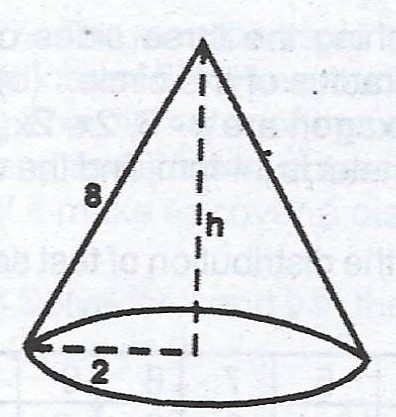
\(h^{2} = 8^{2} - 2^{2}\)
\(h^{2} = 64 - 4 = 60\)
\(h = \sqrt{60}\)
= \(7.746 cm\)
(iii) volume of a cone = \(\frac{1}{3} \pi r^{2} l\)
= \(\frac{1}{3} \times \frac{22}{7} \times 2 \times 2 \times 7.746\)
= \(\frac{88 \times 7.746}{21}\)
= \(32.46 cm^{3}\)
(b)(i) \(100,000 cm = 1 km\)
1 cm represents 20,000 metres
\(\therefore 4.5 cm = (4.5 \times 20,000) cm\)
= 90,000 cm
Converting to km,
= \(\frac{90,000}{100,000}\)
= 0.9km
(ii) 1 metre represents 20,000 metres
16km = 16000m
Distance on the map in metres = \(\frac{16000}{20000}\)
= 0.8m
(iii) Area of the forest on the map
= \(\frac{85 \times (10^{5})^{2} cm^{2}}{(20000)^{2}}\)
= \(\frac{85 \times 10^{10}}{4 \times 10^{8}}\)
= \(2125 cm^{2}\)

