Mathematics JAMB, WAEC, NECO AND NABTEB Official Past Questions

In a college, the number of absentees recorded over a period of 30 days was as shown in the frequency distribution table

Calculate the : (a) Mean

(b) Standard deviation , correct to two decimal places.

(a) The 3rd and 8th terms of an arithmetic progression (A.P) are -9 and 26 respectively. Find the : (i) common difference ; (ii) first term.

(b)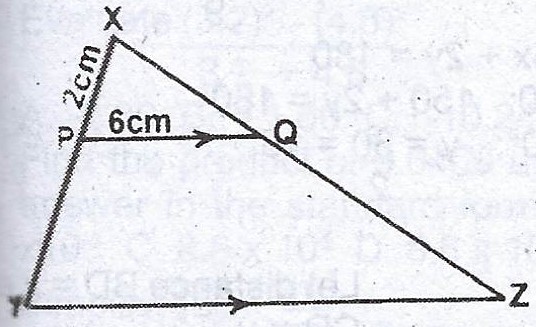 

In the diagram \(\overline{PQ} || \overline{YZ}\), |XP| = 2cm, |PY| = 3 cm, |PQ| = 6 cm and the area of \(\Delta\) XPQ = 24\(cm^{2}\).Calculate the area of the trapezium PQZY.

(a)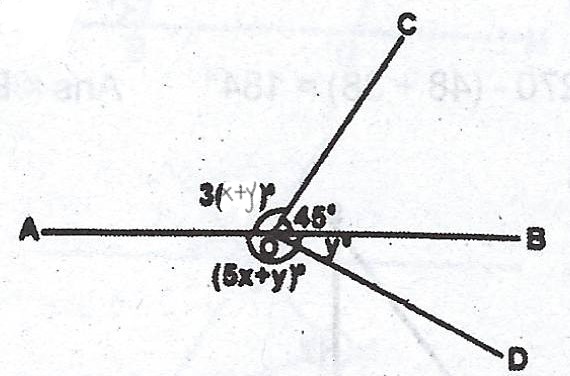 

In the diagram, AOB is a straight line. < AOC = 3(x + y)°, < COB = 45°, < AOD = (5x + y)° and < DOB = y°. Find the values of x and y.

(b) From two points on opposite sides of a pole 33m high, the angles of elevation of the top of the pole are 53° and 67°. If the two points and the base are on te same horizontal level, calculate, correct to three significant figures, the distance between the two points.

(a) Simplify : \(\frac{x^{2} – y^{2}}{3x + 3y}\)

(b)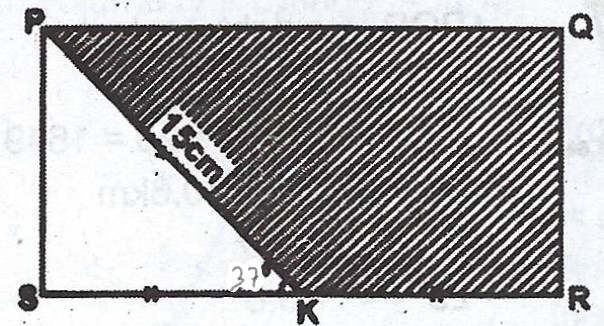 

In the diagram, PQRS is a rectangle. /PK/ = 15 cm, /SK/ = /KR/ and <PKS = 30°. Calculate, correct to three significant figures : (i) /PS/ ; (ii) /SK/ and (iii) the area of the shaded portion.

(a) Using a ruler and a pair of compasses only, construc :

(i) a triangle PQR such that /PQ/ = 10 cm, /QR/ = 7 cm and < PQR = 90° ; (ii) the locus \(l_{1}\) of points equidistant from Q and R ; (iii) the locus \(l_{2}\) of points equidistant from P and Q.

(b) Locate the point O equidistant from P, Q and R.

(c) With O as centre, draw the circumcircle of the triangle PQR.

(d) Measure the radius of the circumcircle.

(a) A cylinder with radius 3.5 cm has its two ends closed, if the total surface area is \(209 cm^{2}\), calculate the height of the cylinder. [Take \(\pi = \frac{22}{7}\)].

(b) 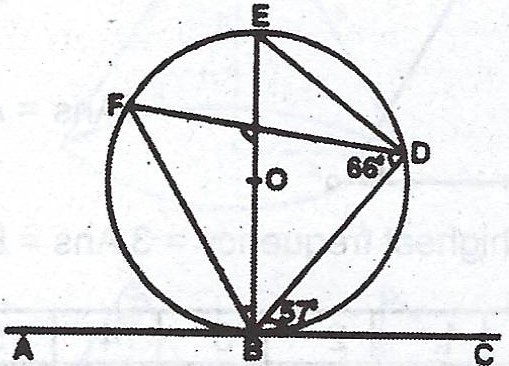 In the diagram, O is the centre of the circle and ABC is a tangent at B. If \(\stackrel\frown{BDF} = 66°\) and \(\stackrel\frown{DBC} = 57°\), calculate, (i) \(\stackrel\frown{EBF}\) and (ii) \(\stackrel\frown{BGF}\).

(a) With the aid of four- figure logarithm tables, evaluate \((0.004592)^{\frac{1}{3}}\).

(b) If \(\log_{10} y + 3\log_{10} x = 2\), express y in terms of x.

(c) Solve the equations : \(3x – 2y = 21\)

                                        \(4x + 5y = 5\).

(a) Simplify : \(\frac{3\frac{1}{12} + \frac{7}{8}}{2\frac{1}{4} – \frac{1}{6}}\)

(b) If \(p = \frac{m}{2} – \frac{n^{2}}{5m}\) ; 

(i) make n the subject of the relation ;  (ii) find, correct to three significant figures, the value of n when p = 14 and m = -8.

Out of the 24 apples in a box, 6 are bad. If three apples are taken from the box at random, with replacement, find the probability that :

(a) the first two are good and the third is bad ;

(b) all three are bad ;

(c) all the three are good.

Y is 60 km away from X on a bearing of 135°. Z is 80 km away from X on a bearing of 225°. Find the :

(a) distance of Z from Y ;

(b) bearing of Z from Y.

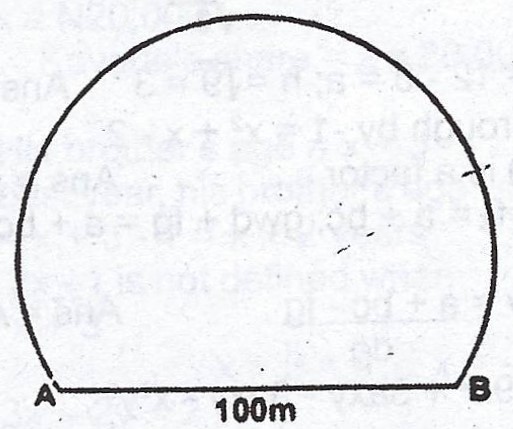
The diagram shows the cross- section of a railway tunnel. If |AB| = 100m and the radius of the arc is 56m, calculate, correct to the nearest metre, the perimetre of the cross- section.

(a) Simplify : \(\frac{x^{2} – 8x + 16}{x^{2} – 7x + 12}\).

(b) If \(\frac{1}{2}, \frac{1}{x}, \frac{1}{3}\) are successive terms of an arithmetic progression (A.P), show that \(\frac{2 – x}{x – 3} = \frac{2}{3}\).

(a) Evaluate, without using mathematical tables or calculator, \((3.69 \times 10^{5}) \div (1.64 \times 10^{-3})\), leaving your answer in standard form.

(b) A man invested N20,000 in bank A and N25,000 in bank B at the beginning of the year. Bank A pays simple interest at a rate of y% per annum and B pays 1.5y% per annum. If his total interest at the end of the year from the two banks was N4,600, find the value of y.

Convert 42₅ to base three numeral

Find the product of 0.0409 and 0.0021 leaving your answer in the standard form

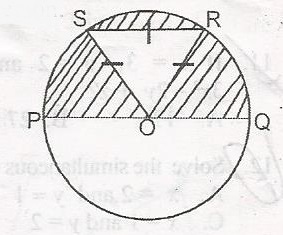
In the diagram, O is the centre of the circle and PQ is a diameter. Triangle RSO is an equilateral triangle of side 4cm. Find the area of the shaded region

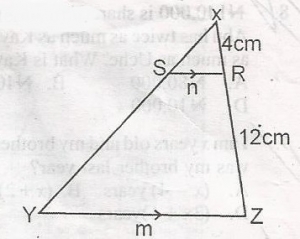
In the diagram, |XR| = 4cm

|RZ| = 12cm, |SR| = n, |XZ| = m and SR||YZ. Find m in terms of n

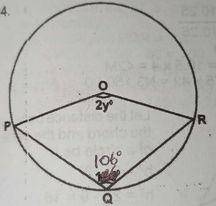
In the diagram, O is the centre of the circle and < PQR = 106º, find the value of y

If the ratio x:y = 3:5 and y:z = 4:7, find the ratio x:y:z

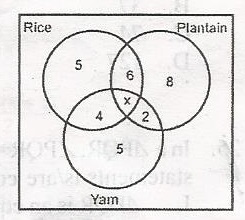
The venn diagram shows the choice of food of a number of visitors to a canteen. How many people took at least two kinds of food?  If there were 35 visitors in all

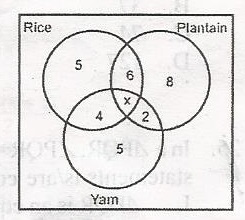
The venn diagram shows the choice of food of a number of visitors to a canteen. If there were 35 visitors in all, find the value of x