Y is 60 km away from X on a bearing of 135°. Z is 80 km away from X on a bearing of 225°. Find the :
(a) distance of Z from Y ;
(b) bearing of Z from Y.
Explanation
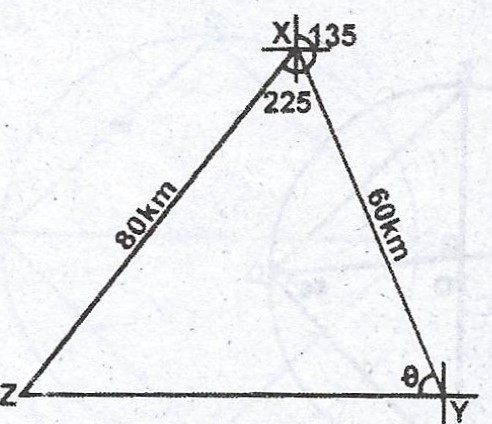
(a) < ZXY = 225° - 135°
= 90°.
\(\therefore /ZY/ = 80^{2} + 60^{2}\)
= \(6400 + 3600 = 10000\)
\(/ZY/ = \sqrt{10000}\)
= 100 km.
(b) From \(\Delta\) XYZ,
\(\tan \theta = \frac{opp}{adj}\)
\(\tan \theta = \frac{80}{60} = 1.333\)
\(\theta = \tan^{-1} (1.333)\)
\(\theta = 53.13°\)
Bearing of Z from Y = \(360° - (45° + 53.13°)\)
= \(360° - 98.13°\)
= \(261.87° \approxeq 262°\) (3 significant figures)

