(a) A cylinder with radius 3.5 cm has its two ends closed, if the total surface area is \(209 cm^{2}\), calculate the height of the cylinder. [Take \(\pi = \frac{22}{7}\)].
(b)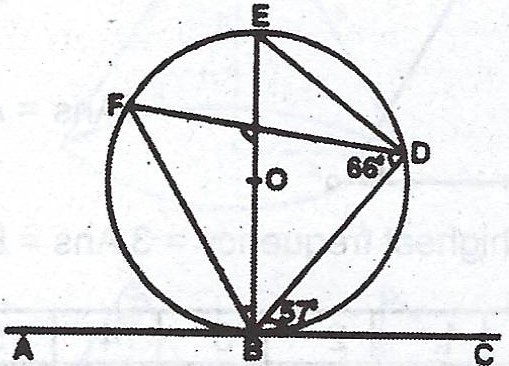 
In the diagram, O is the centre of the circle and ABC is a tangent at B. If \(\stackrel\frown{BDF} = 66°\) and \(\stackrel\frown{DBC} = 57°\), calculate, (i) \(\stackrel\frown{EBF}\) and (ii) \(\stackrel\frown{BGF}\).
Explanation
(a) TSA of a closed cylinder = \(2\pi r^{2} + 2\pi rh\)
= \(2\pi r (r + h)\)
\(2 \times \frac{22}{7} \times 3.5 (3.5 + h) = 209\)
\(22(3.5 + h) = 209 \implies 77 + 22h = 209\)
\(22h = 209 - 77 = 132\)
\(h = \frac{132}{22} = 6 cm\)
(b) \(< EDB = 90°\) (angle subtended at the circumference by a semi-circle)
\(\therefore < EDF = 90° - 66° = 24°\)
\(< EDF = < EBF = 24°\) (angles in the same segment)
(ii)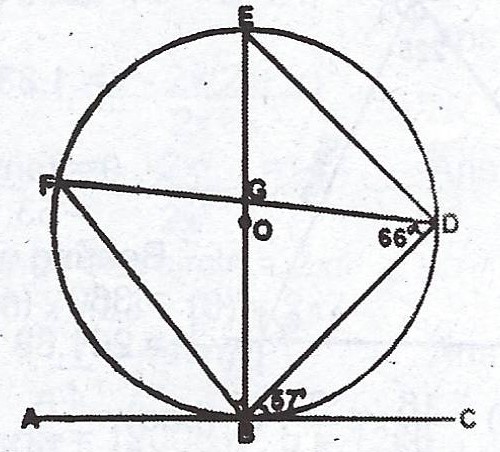 
\(< DEB = < DBC = 57°\) (Alternate segment theorem)
\(\therefore < BGF = 180 - (57 + 24) = 180 - 81\)
\(< BGF = 99°\)