(a) 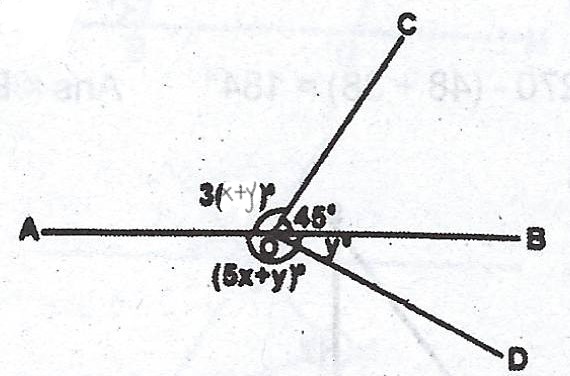
In the diagram, AOB is a straight line. < AOC = 3(x + y)°, < COB = 45°, < AOD = (5x + y)° and < DOB = y°. Find the values of x and y.
(b) From two points on opposite sides of a pole 33m high, the angles of elevation of the top of the pole are 53° and 67°. If the two points and the base are on te same horizontal level, calculate, correct to three significant figures, the distance between the two points.
Explanation
(a) \(3(x + y) + 45 = 180°\) ( sum of angles on a straight line)
\(3x + 3y + 45 = 180 \implies 3x + 3y = 135\)
\(3x = 135 - 3y \implies x = 45 - y\)
Also,
\(5x + y + y = 180\)
\(5x + 2y = 180..... (*)\)
Put x = 45 - y into (*) above,
\(5(45 - y) + 2y = 180 \implies 225 - 5y + 2y = 180\)
\(225 - 3y = 180 \implies 3y = 45\)
\(y = \frac{45}{3} = 15°\)
\(x = 45 - y\)
\(x = 45 - 15 = 30°\)
(b) 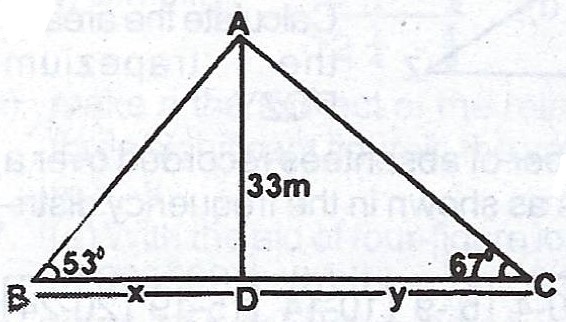
Let the distance BD = x and CD = y.
In \(\Delta ABD\),
\(\tan 53 = \frac{33}{x}\)
\(x = \frac{33}{\tan 53}\)
= \( 24.868 cm\)
In \(\Delta ACD\),
\(\tan 67 = \frac{33}{y}\)
\(y = \frac{33}{\tan 67}\)
\(y = 14.01 cm\)
\(\therefore BC = x + y \)
\(24.868 + 14.01 = 38.878 cm\)
\(\approxeq 38.9 cm\)

