(a) If 3, x, y, 18 are the terms of an Arithmetic Progression (A.P), find the values of x and y.
(b)(i) The sum of the second and third terms of a grometric progression is six times the fourth term. Find the two possible values of the common ratio.
(ii) If the second term is 8 and the common ratio is positive, find the first six terms.
(a) Copy and complete the table of values for \(y = 3\sin x + 2\cos x\) for \(0° \leq x \leq 360°\).
| x | 0° | 60° | 120° | 180° | 240° | 300° | 360° |
| y | 2.00 | 2.00 |
(b) Using a scale of 2 cm to 60° on x- axis and 2 cm to 1 unit on the y- axis, draw the graph of \(y = 3 \sin x + 2 \cos x\) for \(0° \leq x \leq 360°\).
(c) Use your graph to solve the equation : \(3 \sin x + 2 \cos x = 1.5\).
(d) Find the range of values of x for which \(3\sin x + 2\cos x < -1\).
(a) 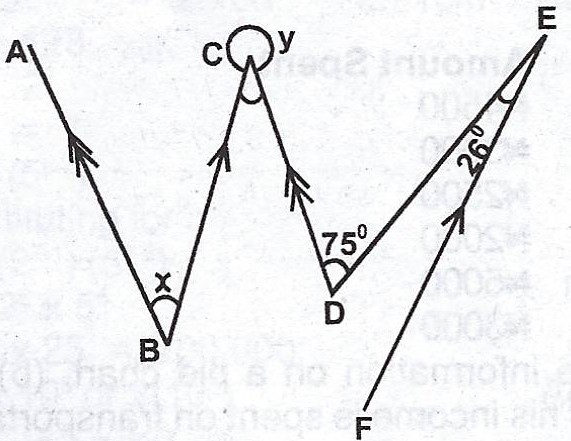
In the diagram, AB // CD and BC // FE. \(\stackrel\frown{CDE} = 75°\) and \(\stackrel\frown{DEF} = 26°\). Find the angles marked x and y.
(b) 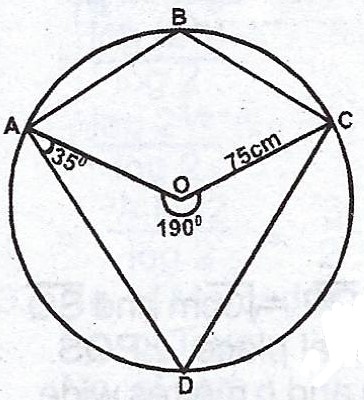
The diagram shows a circle ABCD with centre O and radius 7 cm. The reflex angle AOC = 190° and < DAO = 35°. Find :
(i) < ABC ; (ii) < ADC.
(c) Using the diagram in (b) above, calculate, correct to 3 significant figures, the length of : (i) arc ABC ; (ii) the chord AD. [Take \(\pi = 3.142\)].
(a) Using ruler and a pair of compasses only, construct :
(i) a quadrilateral PQRS such that /PQ/ = 7 cm, < QPS = 60°, /PS/ = 6.5 cm, < PQR = 135° and /QS/ = /QR/ ;
(ii) locus, \(l_{1}\) of points equidistant from P and Q ;
(iii) locus, \(l_{2}\) of points equidistant from P and S.
(b)(i) Label the point T where \(l_{1}\) and \(l_{2}\) intersect. (ii) With center T and radius /TP/, construct a circle \(l_{3}\).
(a) The triangle ABC has sides AB = 17m, BC = 12m and AC = 10m. Calculate the :
(i) largest angle of the triangle ; (ii) area of the triangle.
(b) From a point T on a horizontal ground, the angle of elevation of the top R of a tower RS, 38m high is 63°. Calculate, correct to the nearest metre, the distance between T and S.
The ages, in years, of 50 teachers in a school are given below :
21 37 49 27 49 42 26 33 46 40 50 29 23 24 29 31 36 22 27 38 30 26 42 39 34 23 21 32 41 46 46 31 33 29 28 43 47 40 34 44 26 38 34 49 45 27 25 33 39 40
(a) Form a frequency distribution table of the data using the intervals : 21 – 25, 26 – 30, 31 – 35 etc.
(b) Draw the histogram of the distribution
(c) Use your histogram to estimate the mode
(d) Calculate the mean age.
(a) Solve, correct to two decimal places, the equation \(4x^{2} = 11x + 21\).
(b) A man invests £1500 for two years at compound interest. After one year, his money amounts to £1560. Find the :
(i) rate of interest ; (ii) interest for the second year.
(c) A car costs N300,000.00. It depreciates by 25% in the first year and 20% in the second year. Find its value after 2 years.
(a) If \(2^{x + y} = 16\) and \(4^{x – y} = \frac{1}{32}\), find the value of x and y.
(b) P, Q and R are related in such a way that \(P \propto \frac{Q^{2}}{R}\). When P = 36, Q = 3 and R = 4. Calculate Q when P = 200 and R = 2.
(a) A rectangular field is l metres long and b metres wide. Its perimeter is 280 metres. If the length is two and a half times the breadth, find the values of l and b.
(b) The base of a pyramid is a 4.5 metres rectangle. The height of the pyramid is 4 metres. Calculate its volume.
(a) A pentagon is such that one of its exterior sides is 60°. Two others are (90 – m)° each while the remaining angles are (30 + 2m)° each. Find the value of m.
(b) 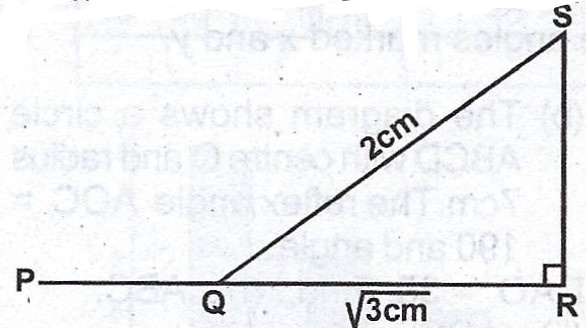
In the diagram, PQR is a straight line, \(\overline{QR} = \sqrt{3} cm\) and \(\overline{SQ} = 2 cm\). Calculate, correct to one decimal place, < PQS.
The table below shows how a man spends his income in a month.
| Items | Amount Spent |
| Food | N4500 |
| House Rent | N3000 |
| Provisions | N2500 |
| Electricity | N2000 |
| Transportation | N5000 |
| Others | N3000 |
(a) Represent the information on a pie chart.
(b) What percentage of his income is spent on transportation?
(a) Solve the inequality : \(\frac{2}{5}(x – 2) – \frac{1}{6}(x + 5) \leq 0\).
(b) Given that P = \(\frac{x^{2} – y^{2}}{x^{2} + xy}\),
(i) express P in its simplest form ; (ii) find the value of P if x = -4 and y = -6.
(a) Without using calculator or tables, find the value of \(\log 3.6\) given that \(\log 2 = 0.3010, \log 3 = 0.4771\) and \(\log 5 = 0.6990\).
(b) If all numbers in the equation \(\frac{y}{y + 101} = \frac{11}{10010}\) are in base two, solve for y.
Every staff in an office owns either a Mercedes and/or a Toyota car. 20 own Mercedes, 15 own Toyota and 5 own both. How many staff are there in the office?
- A. 25
- B. 30
- C. 35
- D. 45
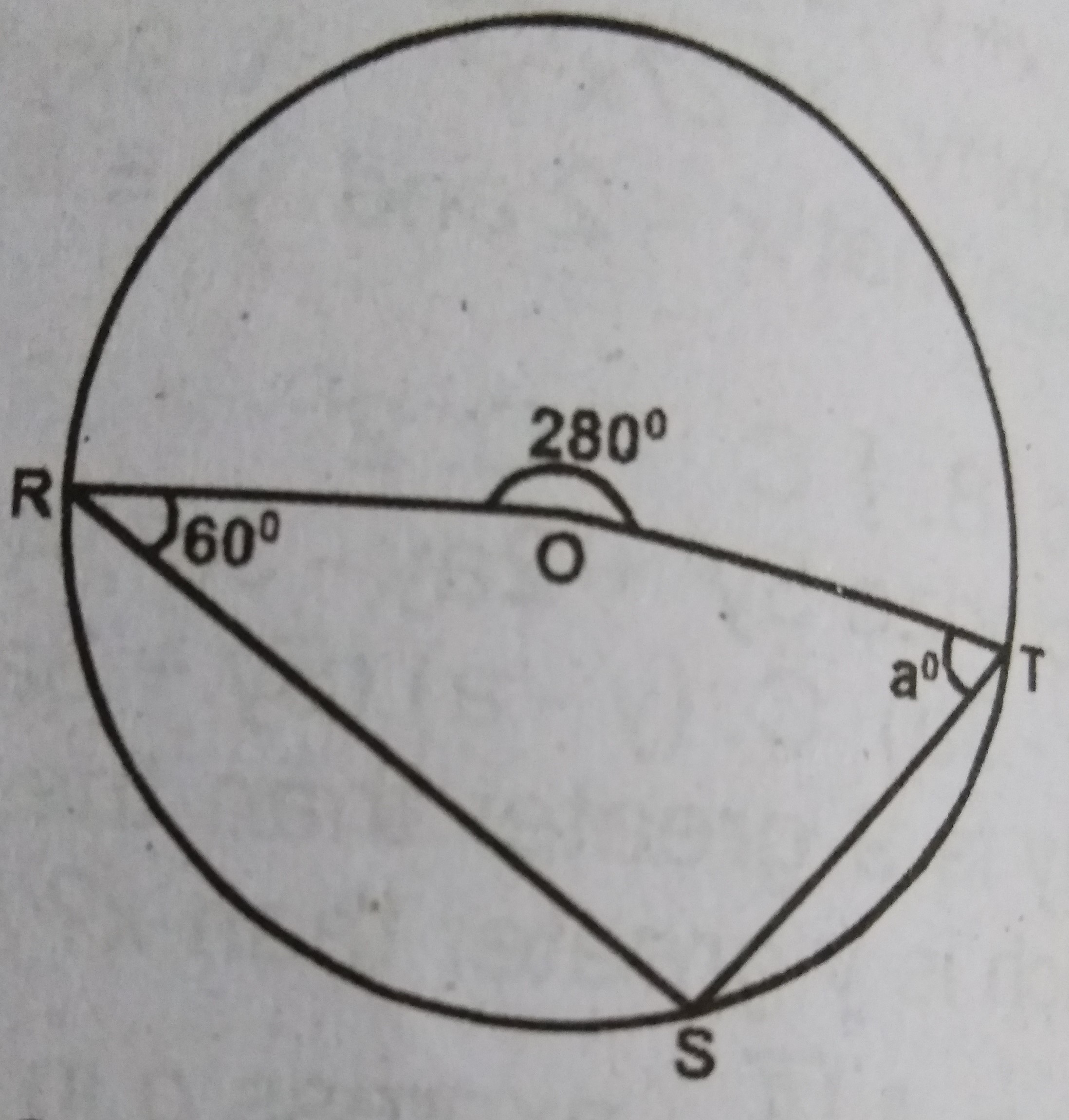
In the diagram, find the size of the angle marked a°
- A. 60o
- B. 80o
- C. 120o
- D. 160o
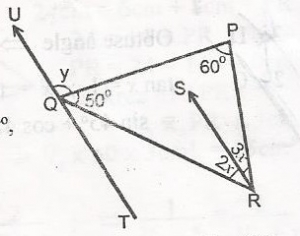
In the diagram, < QPR = 60o
< PQR = 50o
< QRS = 2xo
< SRP = 3xo
< UQP = yo and RS//TU
calculate y
- A. 102o
- B. 78o
- C. 70o
- D. 60o
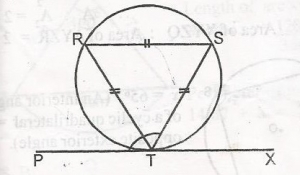
In the diagram, PX is a tangent to the circle and RST is an equilateral triangle. Calculate < PTS
- A. 60o
- B. 90o
- C. 120o
- D. 150o
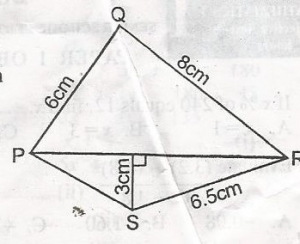
If the perimeter of \(\bigtriangleup\)PQR in thr diagram is 24cm, what is the area of \(\bigtriangleup\)PRS?
- A. 19.5cm2
- B. 15.0cm2
- C. 13.0cm2
- D. 9.3cm2
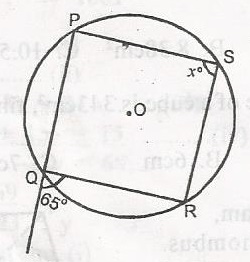
In the diagram, O is the centre of the circle and PQRS is a cyclic quadrilateral. Find the value of x.
- A. 25o
- B. 65o
- C. 115o
- D. 130o
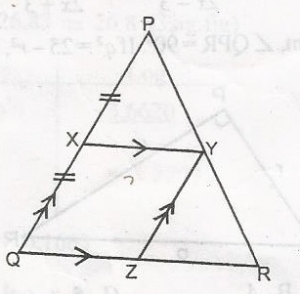
In the figure /PX/ = /XQ/, PQ//YZ and XV//QR. What is the ratio of the area of XYZQ to the area of \(\bigtriangleup\)YZR?
- A. 1:2
- B. 2:1
- C. 1:3
- D. 3:1
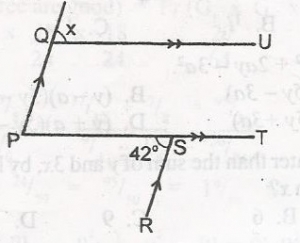
In the diagram, PQ//RS, QU//PT and < PSR = 42o. Find angle x.
- A. 84o
- B. 48o
- C. 42o
- D. 32o


