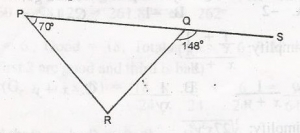
In the figure shown, PQs is a straight line. What is the value of < PRQ?
- A. 128o
- B. 108o
- C. 98o
- D. 78o
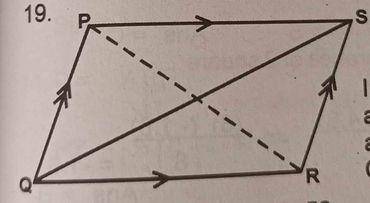
In the diagram above, PQRS is a rhombus. /PR/ = 10cm and /QS/ = 24cm. Calculate the perimeter of the rhombus.
- A. 34cm
- B. 52cm
- C. 56cm
- D. 96cm
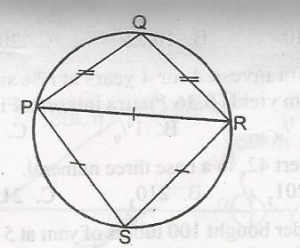
In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS
- A. 150o
- B. 120o
- C. 90o
- D. 60o
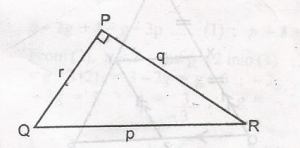
In the diagram, < QPR = 90o. If q2 = 25 – r2. Find the value of p
- A. 3
- B. 4
- C. 5
- D. 6
Find the mean deviation of these numbers 10, 12, 14, 15, 17, 19.
- A. 2.5
- B. 2.6
- C. 2.7
- D. 2.8
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their difference is 6 or 7?
- A. \(\frac{1}{256}\)
- B. \(\frac{1}{16}\)
- C. \(\frac{1}{8}\)
- D. \(\frac{1}{2}\)
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their product is odd?
- A. 1
- B. \(\frac{3}{4}\)
- C. \(\frac{1}{4}\)
- D. zero
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is selected at random from set B, what is the probability that the number is prime?
- A. 1
- B. \(\frac{3}{4}\)
- C. \(\frac{1}{2}\)
- D. \(\frac{1}{4}\)
Solve the inequality 1 – 2x < – \(\frac{1}{3}\)
- A. x < \(\frac{2}{3}\)
- B. x < -\(\frac{2}{3}\)
- C. x > \(\frac{2}{3}\)
- D. x > -\(\frac{2}{3}\)
Find the quadratic equation whose roots are c and -c
- A. x2 - c2 = 0
- B. x2 + 2cx = 0
- C. x2 + 2cx + c2 = 0
- D. x2 - 2cx + c2 = 0
If p = \(\frac{1}{2}\) and \(\frac{1}{p – 1} = \frac{2}{p + x}\), find the value of x
- A. -2\(\frac{1}{2}\)
- B. -1\(\frac{1}{2}\)
- C. 1\(\frac{1}{2}\)
- D. 2\(\frac{1}{2}\)
XY is a chord of circle centre O and radius 7cm. The chord XY which is 8cm long subtends an angle of 120o at the centre of the circle. Calculate the perimeter of the minor segment. [Take \(\pi = \frac{22}{7}\)]
- A. 14.67cm
- B. 22.67cm
- C. 29.33cm
- D. 37.33cm
What is the length of an edge of a cube whose total surface area is X cm2 and whose total surface area is \(\frac{X}{2}\)cm3?
- A. 3
- B. 6
- C. 9
- D. 12
An arc of a circle, radius 14cm, is 18.33cm long. Calculate to the nearest degree, the angle which the arc subtends at the centre of the circle. [T = \(\frac{22}{7}\)]
- A. 11o
- B. 20o
- C. 22o
- D. 75o
A train travels 60km in M minutes. If its average speed is 400km per hour, find the value of M
- A. 15
- B. 12
- C. 10
- D. 9
Simplify \(\frac{\log \sqrt{8}}{\log 4 – \log 2}\)
- A. \(\frac{2}{3}\)
- B. \(\frac{1}{2} \log 2\)
- C. \(\frac{3}{2}\)
- D. \(\log 2\)
If x \(\alpha\) (45 + \(\frac{1}{2}y\)), which of the following is true>?
- A. x varies directly as y
- B. x varies inversely as y
- C. x is partly constant and partly varies as y
- D. x vries jointly as 45 and directly as y
If \(2^n = 128\), find the value of \(2^{n – 1})(5^{n – 2})\)
- A. 5(106)
- B. 2(106)
- C. 5(105)
- D. 2(105)
If cos (x + 25)o = sin 45o, find the value of x
- A. 20
- B. 30
- C. 45
- D. 60
If tan x = 1, evaluate sin x + cos x, leaving your answer in the surd form
- A. 2\(\sqrt{2}\)
- B. \(\frac{1}{2} \sqrt{2}\)
- C. \(\sqrt{2}\)
- D. 2
If xo is obtuse, which of the following is true?
- A. x . 90
- B. 180 < x < 270
- C. x < 90
- D. 90 < x < 180


