(a) How many numbers between 75 and 500 are divisible by 7?
(b) The 8th term of an Arithmetic Progression (A.P) is 5 times the 3rd term while the 7th term is 9 greater than the 4th term. Write the first 5 terms of the A.P.
(a) Copy and complete the table of values for \(y = \sin x + 2 \cos x\), correct to one decimal place.
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° |
240° |
| y | 2.2 | -1.2 | -2.0 | -1.9 |
(b) Using a scale of 2 cm to 30° on the x- axis and 2 cm to 0.5 units on the y- axis, draw the graph of \(y = \sin x + 2\cos x\) for \(0° \leq x \leq 240°\).
(c) Use your graph to solve the equation : (i) \(\sin x + 2 \cos x = 0\) ; (ii) \(\sin x = 2.1 – 2\cos x\).
(d) From the graph, find y when x = 171°.
(a) A circle is inscribed in a square. If the sum of the perimeter of the square and the circumference of the circle is 100 cm, calculate the radius of the circle. [Take \(\pi = \frac{22}{7}\)].
(b) A rope 60cm long is made to form a rectangle. If the length is 4 times its breadth, calculate, correct to one decimal place, the :
(i) length ; (ii) diagonal of the rectangle.
(a) Using ruler and a pair of compasses only, construct : (i) quadrilateral PQRS such that /PQ/ = 10 cm, /QR/ = 8 cm, /PS/ = 6 cm, < PQR = 60° and < QPS = 75° ;
(ii) the locus \(l_{1}\) of points equidistant from QR and RS ; (iii) locus \(l_{2}\) of points equidistant from R and S ;
(b) Measure /RS/.
(a) Simplify \(\frac{x + 2}{x – 2} – \frac{x + 3}{x – 1}\)
(b) The graph of the equation \(y = Ax^{2} + Bx + C\) passes through the point (0, 0), (1, 4) and (2, 10). Find the :
(i) value of C ; (ii) values of A and B ; (iii) co-ordinates of the other point where the graph cuts the x- axis.
The marks scored by 50 students in a Geography examination are as follows :
60 54 40 67 53 73 37 55 62 43 44 69 39 32 45 58 48 67 39 51 46 59 40 52 61 48 23 60 59 47 65 58 74 47 40 59 68 51 50 50 71 51 26 36 38 70 46 40 51 42.
(a) Using class intervals 21 – 30, 31 – 40, …, prepare a frequency distribution table.
(b) Calculate the mean mark of the distribution.
(c) What percentage of the students scored more than 60%?
(a) A woman looking out from the window of a building at a height of 30m, observed that the angle of depression of the top of a flag pole was 44°. If the foot of the pole is 25m from the foot of the building and on the same horizontal ground, find, correct to the nearest whole number, the (i) angle of depression of the foot of the pole from the woman ; (ii) height of the flag pole.
(b) 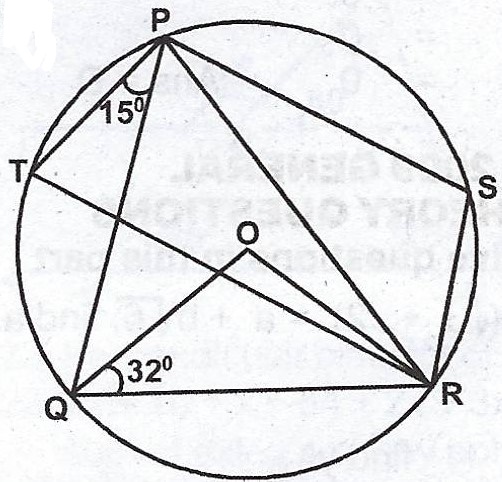 In the diagram, O is the centre of the circle, < OQR = 32° and < TPQ = 15°. Calculate, (i) < QPR ; (ii) < TQo.
In the diagram, O is the centre of the circle, < OQR = 32° and < TPQ = 15°. Calculate, (i) < QPR ; (ii) < TQo.
(a) If \(\log 5 = 0.6990, \log 7 = 0.8451\) and \(\log 8 = 0.9031\), evaluate \(\log (\frac{35 \times 49}{40 \div 56})\).
(b) For a musical show, x children were present. There were 60 more adults than children. An adult paid D5 and a child D2. If a total of D1280 was collected, calculate the
(i) value of x ; (ii) ratio of the number of children to the number of adults ; (iii) average amount paid per person ; (iv) percentage gain if the organisers spent D720 on the show.
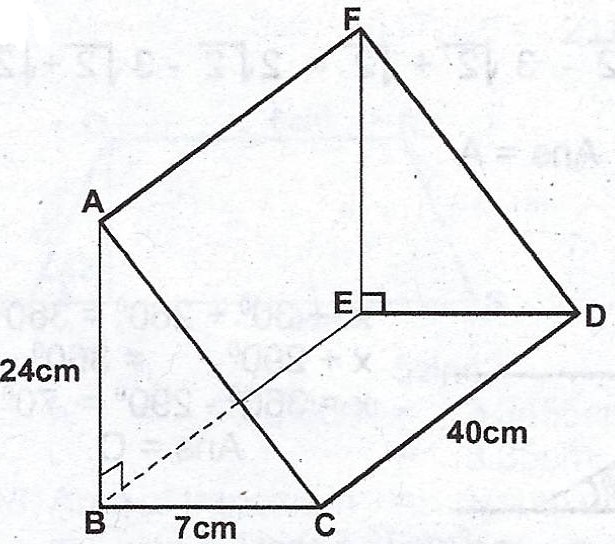
In the diagram, ABCDEF is a triangular prism. < ABC = < DEF = 90°, /AB/ = 24 cm, /BC/ = 7 cm and /CD/ = 40 cm. Calculate :
(a) /AC/ ;
(b) the total surface area of the prism.
(a) Out of 30 candidates applying for a post, 17 have degrees, 15 have diplomas and 4 neither degree nor diploma. How many of them have both?
(b) In triangle PQR, M and N are points on the side PQ and PR respectively such that MN is parallel to QR. If < PRQ = 75°, PN = QN and < PNQ = 125°, determine :
(i) < NQR ; (ii) < NPM.
The table shows the number of children per family in a community.
| No of children | 0 | 1 | 2 | 3 | 4 | 5 |
| No of families | 3 | 5 | 7 | 4 | 3 | 2 |
(a) Find the : (i) mode ; (ii) third quartile ; (iii) probability that a family has at least 2 children.
(b) If a pie chart were to be drawn for the data, what would be the sectorial angle representing families with one child?
(a) If \(9 \cos x – 7 = 1\) and \(0° \leq x \leq 90°\), find x.
(b) Given that x is an integer, find the three greatest values of x which satisfy the inequality \(7x < 2x – 13\).
(a) Given that \((\sqrt{3} – 5\sqrt{2})(\sqrt{3} + \sqrt{2}) = a + b\sqrt{6}\), find a and b.
(b) If \(\frac{2^{1 – y} \times 2^{y – 1}}{2^{y + 2}} = 8^{2 – 3y}\), find y.
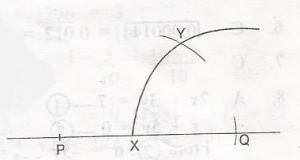
From the diagram which of the following statements are correct? i. XQ is a radius of a circle centre Q. ii. /XQ/ = /QY/. iii. /QX/ = /XY/
- A. i only
- B. inand ii only
- C. ii and iii only
- D. i, ii and iii

The pie chart shows the distribution of 4320 students who graduated from four departments in a university. If a student is picked at random from the four departments, what id the probability that he is not from the education department?
- A. \(\frac{3}{10}\)
- B. \(\frac{2}{9}\)
- C. \(\frac{5}{18}\)
- D. \(\frac{7}{10}\)

The pie chart shows the distribution of 4320 students who graduated from four departments in a university. How many students graduated from the science department?
- A. 840
- B. 864
- C. 920
- D. 960
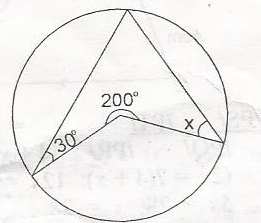
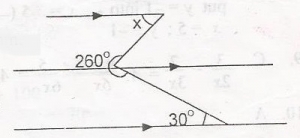
in the diagram, angle 20o is subtended at the centre of the circle, find the value of x
- A. 30o
- B. 50o
- C. 80o
- D. 100o
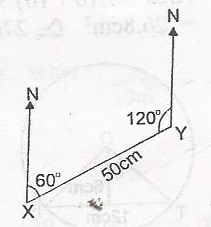
If /XY/ = 50m, how far cast of X is Y?
- A. 25.5m
- B. 40.6m
- C. 40.8m
- D. 43.3m
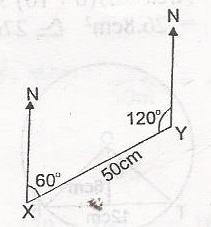
Using the diagram, find the bearing of X from Y
- A. 300o
- B. 240o
- C. 120o
- D. 60o
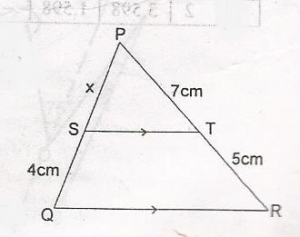
In the diagram, \SQ\ = 4cm, \PT\ = 7cm. /TR/ = 5cm and ST//OR. If /SP/ = xcm, find the value of x
- A. 5.6
- B. 6.5
- C. 6.6
- D. 6.8