(a) The third term of a Geometric Progression (G.P) is 24 and its seventh term is \(4\frac{20}{27}\). Find its first term.
(b) Given that y varies directly as x and inversely as the square of z. If y = 4, when x = 3 and z = 1, find y when x = 3 and z = 2.
The frequency distribution of the weight of 100 participants in a high jump competition is as shown below :
| Weight (kg) | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 – 69 | 70 – 79 |
|
Number of Participants |
10 | 18 | 22 | 25 | 16 | 9 |
(a) Construct the cumulative frequency table.
(b) Draw the cumulative frequency curve.
(c) From the curve, estimate the : (i) median ; (ii) semi- interquartile range ; (iii) probability that a participant chosen at random weighs at least 60 kg.
(a) 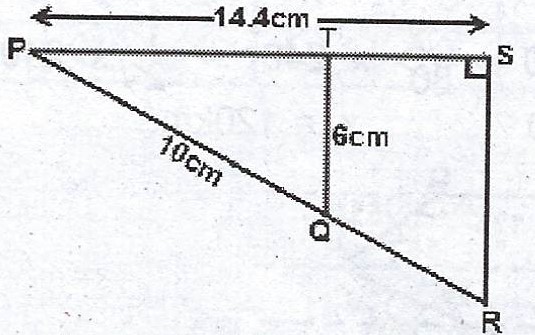
In the diagram, < PTQ = < PSR = 90°, /PQ/ = 10 cm, /PS/ = 14.4 cm and /TQ/ = 6 cm. Calculate the area of the quadrilateral QRST.
(b) Two opposite sides of a square are each decreased by 10% while the other two are each increased by 15% to form a rectangle. Find the ratio of the area of the rectangle to that of the square.
(a) Copy and complete the table of values for the relation \(y = -x^{2} + x + 2; -3 \leq x \leq 3\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -4 | 2 | -4 |
(b) Using scales of 2 cm to 1 unit on the x- axis and 2 cm to 2 units on the y- axis, draw a graph of the relation \(y = -x^{2} + x + 2\).
(c) From the graph, find the : (i) minimum value of y ; (ii) roots of equation \(x^{2} – x – 2 = 0\) ; (iii) gradient of the curve at x = -0.5.
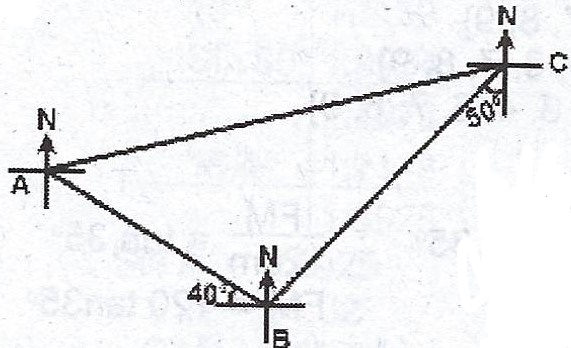 In the diagram, /AB/ = 8 km, /BC/ = 13 km, the bearing of A from B is 310° and the bearing of B from C is 230°. Calculate, correct to 3 significant figures,
In the diagram, /AB/ = 8 km, /BC/ = 13 km, the bearing of A from B is 310° and the bearing of B from C is 230°. Calculate, correct to 3 significant figures,
(a) the distance AC ;
(b) the bearing of C from A ;
(c) how far east of B, C is.
Using ruler and a pair of compasses only,
(a) construct (i) a quadrilateral PQRS with /PS/ = 6 cm, < RSP = 9 cm, /QR/ = 8.4 cm and /PQ/ = 5.4 cm; (ii) the bisectors of < RSP and < SPQ to meet at X ; (iii) the perpendicular XT to meet PS at T.
(b) Measure /XT/.
(a) Madam Kwakyewaa imported a quantity of frozen fish costing GH¢ 400.00. The goods attracted an import duty of 15% of its cost. She also paid a sales tax of 10% of the total cost of the goods including the import duty and then sold the goods for GH¢ 660.00. Calculate the percentage profit.
(b) In a school, there are 1000 boys and a number of girls. The 48% of the total number of students that were successful in an examination was made up of 50%of the boys and 40% of the girls. Find the number of girls in the school.
(a) The scale of a map is 1 : 20,000. Calculate the area, in square centimetres, on the map of a forest reserve which covers 85\(km^{2}\).
(b) A rectangular playing field is 18m wide. It is surrounded by a path 6m wide such that its area is equal to the perimeter of the path. Calculate the length of the field.
(c) 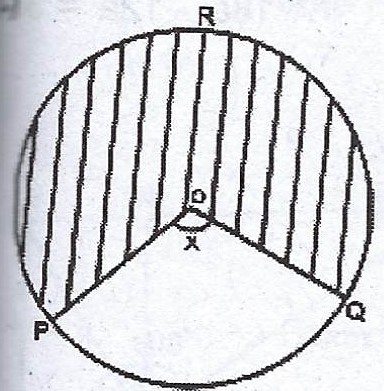 The diagram shows a circle centre O. If < POQ = x°, the diameter of the circle is 7 cm and the area of the shaded portion is 27.5\(cm^{2}\). Find, correct to the nearest degree, the value of x. [Take \(\pi = \frac{22}{7}\)].
The diagram shows a circle centre O. If < POQ = x°, the diameter of the circle is 7 cm and the area of the shaded portion is 27.5\(cm^{2}\). Find, correct to the nearest degree, the value of x. [Take \(\pi = \frac{22}{7}\)].
Two fair die are thrown. M is the event described by “The sum of the scores is 10” and N is the event described by “The difference between the scores is 3”.
(a) Write out the elements of M and N.
(b) Find the probability of M or N.
(c) Are M and N mutually exclusive? Give reasons.
(a) 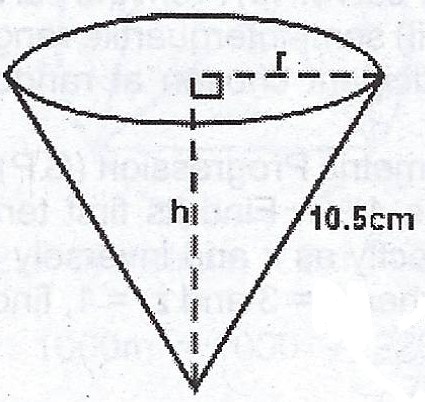
Curved Surface Area = \(\pi rl\)
\(115.5 = \frac{22}{7} \times r \times 10.5\)
\(115.5 = 33r\)
\(r = \frac{115.5}{33} = 3.5 cm\)
(b) 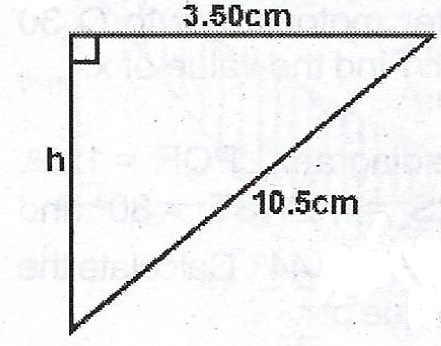
\(\therefore h^{2} + (3.50)^{2} = (10.5)^{2}\)
\(h^{2} = 10.5^{2} – 3.5^{2}\)
\(h^{2} = 98 \implies h = \sqrt{98}\)
\(h = 9.8994 cm \approxeq 9.90 cm\)
(c) Volume of a cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 9.90\)
= \(\frac{23.1 \times 11}{2}\)
= \(127.05 cm^{3} \approxeq 127 cm^{3}\)
(a) 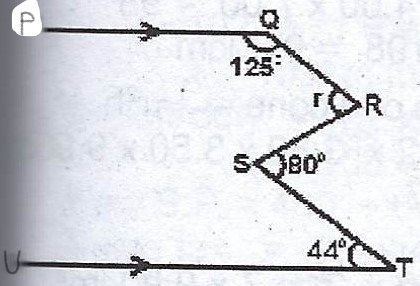
In the diagram, < PQR = 125°, < QRS = r, < RST = 80° and < STU = 44°. Calculate the value of r.
(b) 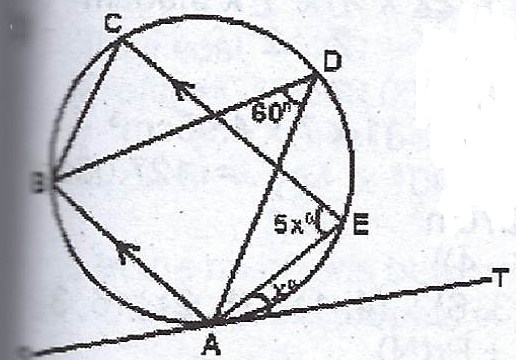 In the diagram TS is a tangent to the circle at A. AB // CE, < AEC = 5x°, < ADB = 60° and < TAE = x. Find the value of x.
In the diagram TS is a tangent to the circle at A. AB // CE, < AEC = 5x°, < ADB = 60° and < TAE = x. Find the value of x.
(a) The angle of depression of a boat from the mid-point of a vertical cliff is 35°. If the boat is 120m from the foot of the cliff, calculate the height of the cliff.
(b) Towns P and Q are x km apart. Two motorists set out at the same time from P to Q at steady speeds of 60 km/h and 80 km/h. The faster motorist got to Q 30 minutes earlier than the other. Find the value of x.
A = {2, 4, 6, 8}, B = {2, 3, 7, 9} and C = {x : 3 < x < 9} are subsets of the universal set U = {2, 3, 4, 5, 6, 7, 8, 9}. Find
(a) \(A \cap (B’ \cap C’)\) ;
(b) \((A \cup B) \cap (B \cup C)\).
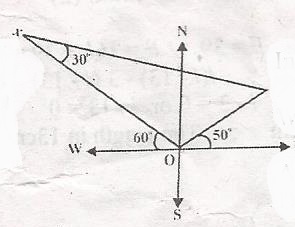
In the diagram, < WOX = 60o, < YOE = 50o and < OXY = 30o. What is the bearing of x from y?
- A. 300o
- B. 240o
- C. 190o
- D. 150o
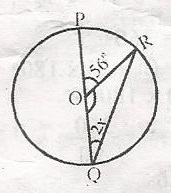
In the diagram, 0 is the centre of the circle. Find the value x
- A. 34
- B. 29
- C. 17
- D. 14
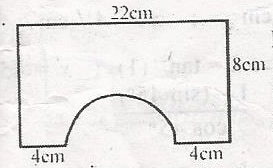
The diagram shows a rectangular cardboard from which a semi-circle is cut off. Calculate the area of the remaining part
- A. 44cm2
- B. 99cm2
- C. 154cm2
- D. 165cm2
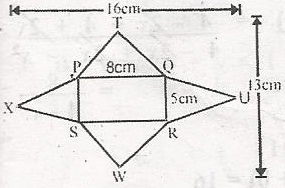
The diagram is a net right rectangular pyramid. Calculate the total surface area
- A. 208cm2
- B. 112cm2
- C. 92cm2
- D. 76cm2
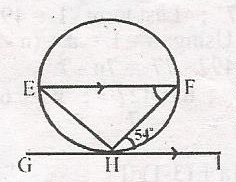
In the diagram, GI is a tangent to the circle at H. If EF//GI, calculate the size of < EHF
- A. 126o
- B. 72o
- C. 64cmo
- D. 32cmo
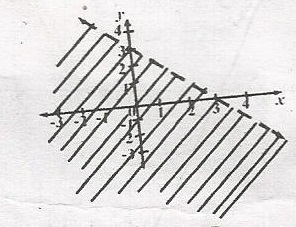
The shaded portion in the diagram is the solution of
- A. x + y \(\leq\) 3
- B. x + y < 3
- C. x + y > 3
- D. x + y \(\geq\) 3
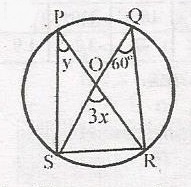
In the diagram, O is the centre of the circle, < SQR = 60o, < SPR = y and < SOR = 3x. Find the value of (x + y)
- A. 110o
- B. 100o
- C. 80o
- D. 70o
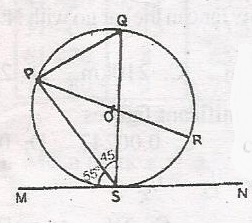
In the diagram, the tangent MN makes an angle of 55o with the chord PS. IF O is the centre of the circle, find < RPS
- A. 55o
- B. 45o
- C. 35o
- D. 25o


