(a) Divide \(\frac{x^{2} – 4}{x^{2} + x}\) by \(\frac{x^{2} – 4x + 4}{x + 1}\).
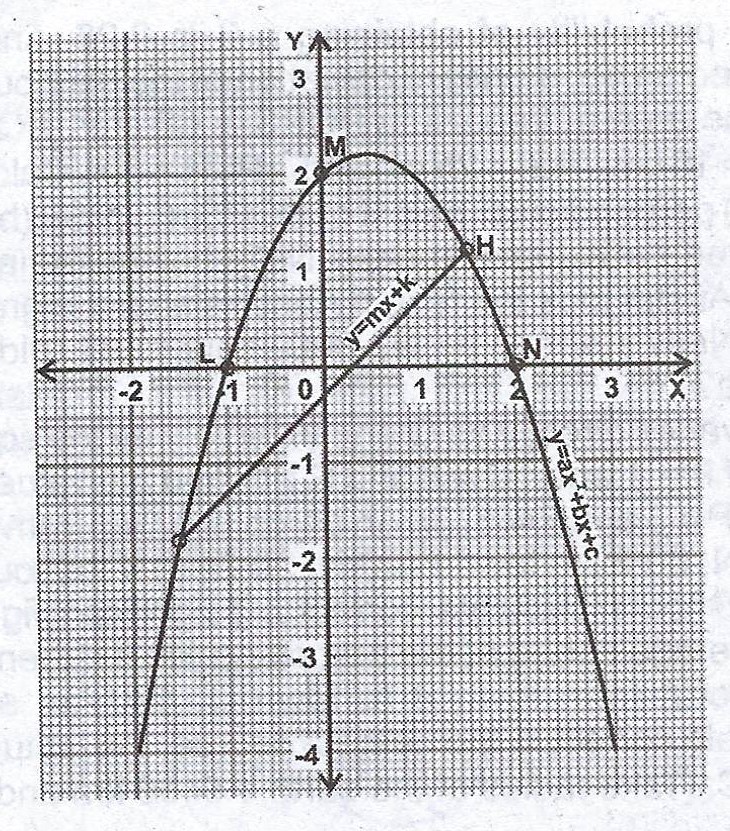
(b) The diagram below shows the graphs of \(y = ax^{2} + bx + c\) and \(y = mx + k\) where a, b, c and m are constants. Use the graph(s) to :
(i) find the roots of the equation \(ax^{2} + bx + c = mx + k\);
(ii) determine the values of a, b and c using the coordinates of points L, M and N and hence write down the equation of the curve;
(iii) determine the line of symmetry of the curve \(y = ax^{2} + bx + c\).
Explanation
(a) \(\frac{x^{2} - 4}{x^{2} + x} \div \frac{x^{2} - 4x + 4}{x + 1}\)
= \(\frac{x^{2} - 4}{x^{2} + x} \times \frac{x + 1}{x^{2} - 4x + 4}\)
= \(\frac{(x - 2)(x + 2)}{x(x + 1)} \times \frac{x + 1}{x^{2} - 2x - 2x + 4}\) (Using difference of two squares)
= \(\frac{(x - 2)(x + 2)}{x} \times \frac{1}{(x - 2)^{2}}\)
= \(\frac{(x + 2)}{x(x - 2)}.
(b) Roots of \(ax^{2} +bx + c = mx + k\)
For graph \(y = ax^{2} + bx + c\),
\(x = -1\) and \(x = 2\)
\(x + 1 = 0\) and \(x - 2 = 0\)
\((x + 1)(x - 2) = 0\)
\(x^{2} - 2x + x - 2 = 0\)
\(x^{2} - x - 2 = 0 ..... (i)\)
\(-x^{2} + x + 2 = 0 ...... (ii)\)
For graph \(y = mx + k\)
\(m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{1 - (-1)}{1.3 - (-1.3)}\)
\(m = \frac{2}{2.6} = 0.769\)
\(k = 0.25\)
\(x^{2} - x - 2 = 0.769x + 0.25\)
\(x^{2} - x - 0.769x - 2 - 0.25 = 0\)
\(x^{2} - 1.769x - 2.25 = 0\)
Using formula method, \(x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\)
\(x = \frac{-(-1.769) \pm \sqrt{(-1.769)^{2} - 4(1)(-2.25)}}{2(1)}\)
\(x = \frac{1.769 \pm \sqrt{3.1294 + 9}}{2}\)
\(x = \frac{1.769 \pm 3.483}{2}\)
\(x = \frac{1.769 + 3.483}{2}\) or \(x = \frac{1.769 - 3.483}{2}\)
\(x = \frac{5.252}{2} \approxeq 2.626\) or \(x = \frac{-1.714}{2} \approxeq -0.857\)
(ii) The coordinates of points L, M and N are (-1, 0), (0, 2) and (2, 0) respectively.
Using coordinate for L:
\(0 = a(-1^{2}) + b(-1) + c \implies 0 = a - b + c ..... (1)\)
Using M :
\(2 = a(0^{2}) + b(0) + c \implies c = 2 ...... (2)\)
Using N :
\(0 = a(2^{2}) + b(2) + c \implies 0 = 4a + 2b + c .... (3)\)
From (2), c = 2
\(\therefore (1) : a - b + 2 = 0 \implies a - b = -2 .... (1a)\)
\(\therefore (3) : 4a + 2b + 2 = 0 \implies 4a + 2b = -2 ..... (3a)\)
Solving equations (1a) and (3a) simultaneously, we get
\(a = -1 , b = 1 , c = 2\)
\(\therefore\) Equation of the curve : \(-x^{2} + x + 2 = 0\)
(iii) Line of symmetry = \(x = \frac{-b}{2a}\)
\(y = -x^{2} + x + 2 \)
Line of symmetry = \(\frac{-1}{2(-1)}\)
\(x = \frac{1}{2}\)

