(a) Given that \(\sin x = 0.6, 0° \leq x \leq 90°\), evaluate \(2\cos x + 3\sin x\), leaving your answer in the form \(\frac{m}{n}\), where m and n are integers.
(b) 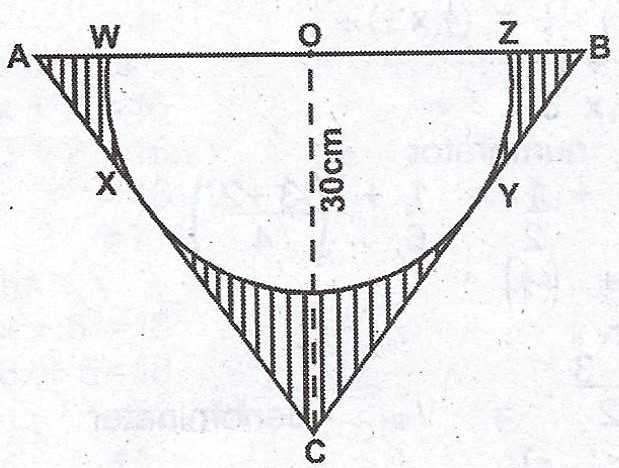
In the diagram, a semi-circle WXYZ with centre O is inscribed in an isosceles triangle ABC. If /AC/ = /BC/, |OC| = 30 cm and < ACB = 130°, calculate, correct to one decimal place, the (i) radius of the circle ; (ii) area oc the shaded portion. [Take \(\pi = \frac{22}{7}\)].
Explanation
Given \(\sin x = 0.6 = \frac{3}{5}\)
\(\therefore Opp = 3; Hyp = 5\)
Using Pythagoras theorem,
\(5^{2} = 3^{2} + Adj^{2}\)
\(Adj = \sqrt{5^{2} - 3^{2}}\)
\(Adj = \sqrt{25 - 9} = \sqrt{16} = 4\)
\(\therefore \cos x = \frac{4}{5} = 0.8\)
\(2\cos x + 3\sin x = 2(\frac{4}{5}) + 3(\frac{3}{5})\)
= \(\frac{8}{5} + \frac{9}{5}\)
= \(\frac{17}{5}\).
(b) 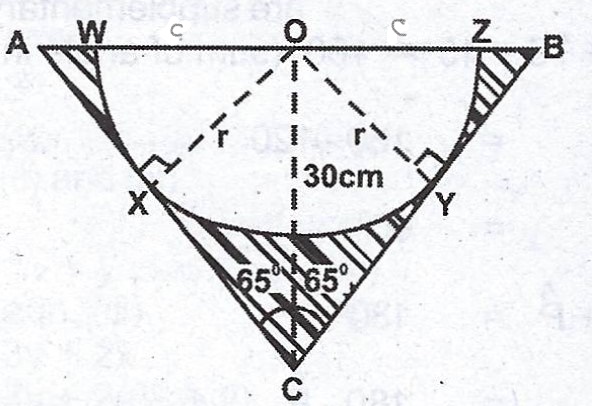
Join O to X and O to Y.
Considering either \(\Delta OXC\) or \(\Delta OYC\),
\(\sin 65 = \frac{r}{30}\)
\(r = 30 \sin 65\)
\(r = 30 \times 0.9063\)
\(r = 27.189 cm \approxeq 27.2 cm\) (to one decimal place)
(b) Area of shaded portion = Area of triangle ABC - Area of semi-circle WXYZ.
= \(\frac{1}{2} bh - \frac{1}{2} \pi r^{2}\)
= \((\frac{1}{2} \times 2c \times 30) - (\frac{1}{2} \times \frac{22}{7} \times (27.189)^{2})\)
From \(\Delta COA, \tan 65 = \frac{c}{30}\)
\(\implies c = 30 \tan 65 \approxeq 64.34 cm\)
\(\therefore\) Area of shaded portion = \(30(64.34) - \frac{8131.659}{7}\)
= \(1930.056 - 1161.666\)
= \(768.39 cm^{2}\)

