(a) The area of trapezium PQRS is 60\(cm^{2}\). PQ // RS, /PQ/ = 15 cm, /RS/ = 25 cm and < PSR = 60°. Calculate the : (i) perpendicular height of PQRS ; (ii) |PS|.
(b) Ade received \(\frac{3}{5}\) of a sum of money, Nelly \(\frac{1}{3}\) of the remainder while Austin took the rest. If Austin’s share is greater than Nelly’s share by N3,000, how much did Ade get?
Explanation
(a) 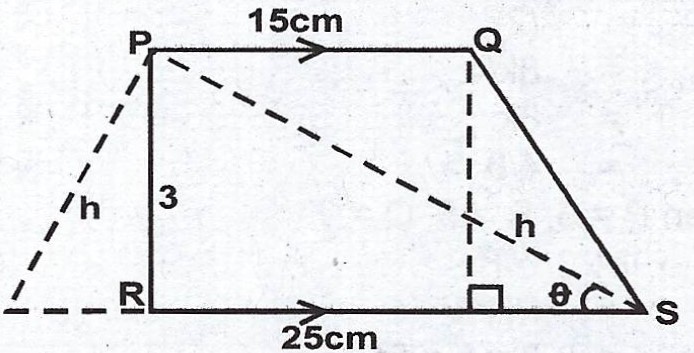
\(\theta = \frac{60°}{2} = 30°\)
Area of trapezium = \(\frac{a + b}{2} h\)
\(60 = \frac{15 + 25}{2} h \implies 60 = 20h\)
\(h = \frac{60}{20} = 3 cm\)
(ii) Considering \(\Delta PSR\),
\(\sin \theta = \frac{Opp}{Hyp}\)
\(\sin 30 = \frac{3}{|PS|}\)
\(|PS| = \frac{3}{\sin 30}\)
= \(\frac{3}{0.5} = 6 cm\)
(b) Let the total amount to be shared = k.
Ade's share = \(\frac{3}{5} k \)
Remainder = \(k - \frac{3}{5}k \)
= \(\frac{2}{5}k\)
Nelly's share : \(\frac{1}{3} \times \frac{2}{5}k\)
= \(\frac{2}{15}k\)
Austin's share : \(\frac{2}{5}k - \frac{2}{15}k\)
= \(\frac{4}{15}k\)
\(\frac{4}{15}k - \frac{2}{15}k = \frac{2}{15}k\)
\(\frac{2}{15}k = N3,000\)
\(\implies k = \frac{3,000 \times 15}{2}\)
= \(N22,500\)
Ade's share = \(\frac{3}{5}k\)
= \(\frac{3}{5} \times N22,500 = N13,500\).

