(a) 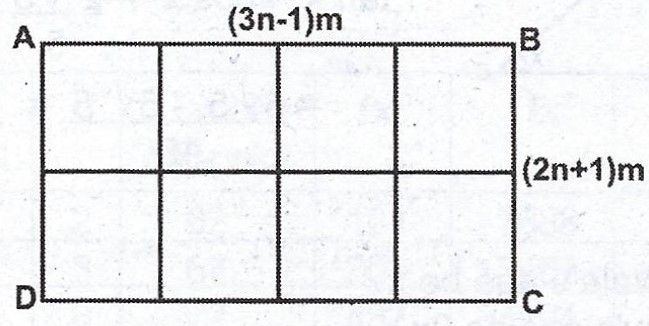
In the diagram, ABCD is a rectangular garden (3n – 1)m long and (2n + 1)m wide. A wire mesh 135m long is used to mark its boundary and to divide it into 8 equal plots. Find the value of n.
(b) A cylinder with base radius 14 cm has the same volume as a cube of side 22 cm. Calculate the ratio of the total surface area of the cylinder to that of the cube. [Take \(\pi = \frac{22}{7}\)]
Explanation
(a) \(3(3n - 1) + 5(2n + 1) = 135\)
\(9n - 3 + 10n + 5 = 135\)
\(19n + 2 = 135\)
\(19n = 135 - 2 = 133\)
\(n = \frac{133}{19} = 7\)
(b) Radius of a cylinder = 14 cm
side of a cube = 22 cm
\(\therefore \frac{22}{7} \times 14 \times 14 \times h = 22 \times 22 \times 22\)
\(44 \times 14 \times h = 22 \times 22 \times 22\)
\(h = \frac{22 \times 22 \times 22}{44 \times 14}\)
= \(\frac{121}{7} cm\)
TSA of a cylinder = \(2\pi r (r + h) = 2 \times \frac{22}{7} \times 14 (14 + \frac{121}{7})\)
= \(88(\frac{98 + 121}{7}) = \frac{88 \times 219}{7}\)
= \(\frac{19272}{7} cm^{2}\)
TSA of a cube = \(6s^{2}\)
= \(6 \times 22 \times 22\)
= \(2904 cm^{2}\)
Ratio = \(\frac{19272}{7} : 2904\)
= \(73 : 77\)

