When one end of a ladder, LM, is placed against a vertical wall at a point 5 metres above the ground, the ladder makes an angle of 37° with the horizontal ground.
(a) Represent this information in a diagram ;
(b) Calculate, correct to 3 significant figures, the length of the ladder ;
(c) If the foot of the ladder is pushed towards the wall by 2 metres, calculate,correct to the nearest degree, the angle which the ladder nows makes with the ground.
An aeroplane flies due North from a town T on the equator at a speed of 950km per hour for 4 hours to another town P. It then flies eastwards to town Q on longitude 65°E. If the longitude of T is 15°E,
(a) represent this information in a diagram ;
(b) calculate the : (i) latitude of P, correct to the nearest degree ; (ii) distance between P and Q, correct to four significant figures. [Take \(\pi = \frac{22}{7}\); Radius of the earth = 6400km].
The frequency distribution table shows the marks obtained by 100 students in a Mathematics test.
|
Marks (%) |
1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
| Frequency | 2 | 3 | 5 | 13 | 19 | 31 | 13 | 9 | 4 | 1 |
(a) Draw the cumulative curve for the distribution.
(b) Use the graph to find the : (i) 60th percentile ; (ii) probability that a student passed the test if the pass mark was fixed at 35%.
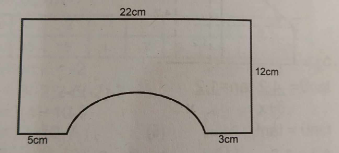
(a)
A segment of a circle is cut off from a rectangular board as shown in the diagram. If the radius of the circle is \(1\frac{1}{2}\) times the length of the chord; calculate, correct to 2 decimal places, the perimeter of the remaining portion. [Take \(\pi = \frac{22}{7}\)]
(b) Evaluate without using calculators or tables, \(\frac{3}{\sqrt{3}}(\frac{2}{\sqrt{3}} – \frac{\sqrt{12}}{6})\).
(a) Using ruler and a pair of compasses only, construct : (i) a trapezium WXYZ such that |WX| = 10.2 cm, |XY| = 5.6 cm, |YZ| = 5.8 cm, < WXY = 60° and WX is parallel to YZ (ii) a perpendicular from Z to meet \(\overline{WX}\) at N.
(b) Measure : (i) |WZ| ; (ii) |ZN| .
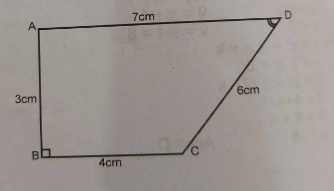
(a) If (3 – x), 6, (7 – 5x) are consecutive terms of a geometric progression (GP) with constant ratio r > 0, find the :
(i) values of x ; (ii) constant ratio.
(b) In the diagram above, |AB| = 3 cm, |BC| = 4 cm, |CD| = 6 cm and |DA| = 7 cm. Calculate
(a) Copy and complete the table of values for the relation \(y = 3x^{2} – 5x – 7\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 35 | -7 | -9 | 5 |
(b) Using scales of 2 cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of \(y = 3x^{2} – 5x – 7, -3 \leq x \leq 4\).
(c) From the graph : (i) find the roots of the equation \(3x^{2} – 5x – 7 = 0\) ; (ii) estimate the minimum value of y ; (iii) calculate the gradient of the curve at the point x = 2.
(a) Two positive whole numbers p and q are such that p is greater than q and their sum is equal to three times their difference;
(i) Express p in terms of q ; (ii) Hence, evaluate \(\frac{p^{2} + q^{2}}{pq}\).
(b) A man sold 100 articles at 25 for N66.00 and made a gain of 32%. Calculate his gain or loss percent if he sold them at 20 for N50.00.
A boy 1.2m tall, stands 6m away from the foot of a vertical lamp pole 4.2m long. If the lamp is at the tip of the pole,
(a) represent this information in a diagram ;
(b) calculate the (i) length of the shadow of the boy cast by the lamp ; (ii) angle of elevation of the lamp from the boy, correct to the nearest degree.
The area of a circle is \(154cm^{2}\). It is divided into three sectors such that two of the sectors are equal in size and the third sector is three times the size of the other two put together. Calculate the perimeter of the third sector. [Take \(\pi = \frac{22}{7}\)].
(a) The present ages of a father and his son are in the ratio 10 : 3. If the son is 15 years old now, in how many years will the ratio of their ages be 2 : 1?
(b) The arithmetic mean of x, y and z is 6 while that of x, y, z, l, u, v and w is 9. Calculate the arithmetic mean of l, u, v and w.
(a) Solve : \(7x + 4 < \frac{1}{2}(4x + 3)\).
(b) Salem, Sunday and Shaka shared a sum of N1,100.00. For every N2.00 that Salem gets, Sunday gets 50 kobo and for every N4.00 Sunday gets, Shaka gets N2.00. Find Shaka’s share.
(a) Simplify, without using tables or calculator : \(\frac{\frac{3}{4}(3\frac{3}{8} + 1\frac{5}{8})}{2\frac{1}{8} – 1\frac{1}{2}}\).
(b) Given that \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), evaluate, correct to 2 significant figures and without using tables or calculator, \(\log_{10} 1.125\).
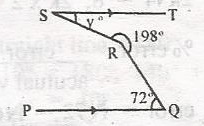
In the diagram, ST//PQ reflex angle SRQ = 198o and < RQp = 72o. Find the value of y
- A. 18o
- B. 54o
- C. 87o
- D. 92o
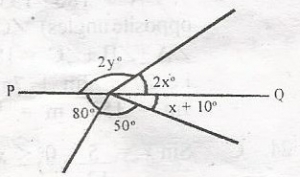
In the diagram, PQ is a straight line. Calculate the value of the angle labelled 2y
- A. 130o
- B. 120o
- C. 110o
- D. 100o
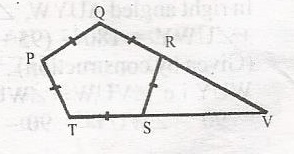
In the diagram, PQRST is a regular polygon with sides QR and TS produced to meet at V. Find the size of < RVS
- A. 36o
- B. 54o
- C. 60o
- D. 72o
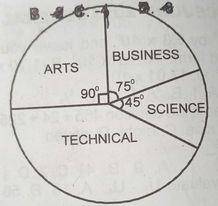
The pie chart shows the distribution of 600 mathematics textbooks for Arts, Business, Science and Technical Classes. What percentage of the total number of textbooks belongs to science?
- A. 12\(\frac{1}{2}\)%
- B. \(\frac{205}{6}\)%
- C. 25%
- D. \(\frac{412}{3}\)%

The pie chart shows the distribution of 600 mathematics textbooks for Arts, Business, Science and Technical Classes. How many textbooks are for the technical class?
- A. 100
- B. 150
- C. 200
- D. 250
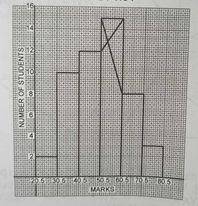
Using the histogram, what is the median class?
- A. 60.5 - 70.5
- B. 50.5 - 60.5
- C. 40.5 - 50.5
- D. 30.5 - 40.5
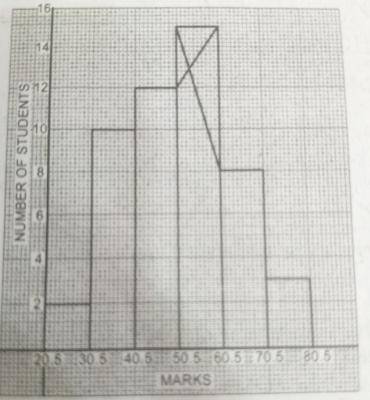
Using the histogram, estimate the mode of distribution
- A. 51.5
- B. 52.5
- C. 53.5
- D. 54.5