The area of a circle is \(154cm^{2}\). It is divided into three sectors such that two of the sectors are equal in size and the third sector is three times the size of the other two put together. Calculate the perimeter of the third sector. [Take \(\pi = \frac{22}{7}\)].
Explanation
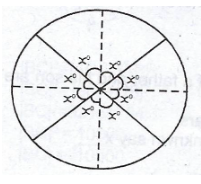
Since it is divided into 3 sectors
then \(8x° = 360°\)
\(x° = 45°\)The 3rd sector = 3 times the size of the other two sectors put together
= \(3(45 + 45) = 3(90) = 270°\)
Perimeter of a sector = \(2r + l\)
where r = radius of the circle ; l = length of arc = \(\frac{\theta}{360°} \times 2\pi r\)
Area of circle = \(\frac{22}{7} \times r^{2} = 154 cm^{2}\)
\(r^{2} = \frac{154 \times 7}{22} = 49\)
\(r = 7 cm\)
\(l = \frac{270}{360} \times 2 \times \frac{22}{7} \times 7 = 33 cm\)
Perimeter of sector = \(2(7) + 33 = 14 + 33 = 47 cm\).

