(a) Two functions, f and g, are defined by \(f : x \to 2x^{2} – 1\) and \(g : x \to 3x + 2\) where x is a real number.
(i) If \(f(x – 1) – 7 = 0\), find the values of x.
(ii) Evaluate : \(\frac{f(-\frac{1}{2}) . g(3)}{f(4) – g(5)}\).
(b) An operation, \((\ast)\) is defined on the set R, of real numbers, by \(m \ast n = \frac{-n}{m^{2} + 1}\), where \(m, n \in R\). If \(-3, -10 \in R\), show whether or not \(\ast\) is commutative.
(a) Given that \(5 \cos (x + 8.5)° – 1 = 0, 0° \leq x \leq 90°\), calculate, correct to the nearest degree, the value of x.
(b) The bearing of Q from P is 0150° and the bearing of P from R is 015°. If Q and R are 24km and 32km respectively from P : (i) represent this information in a diagram;
(ii) calculate the distance between Q and R, correct to two decimal places ; (iii) find the bearing of R from Q, correct to the nearest degree.
| Scores | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 2 | 5 | 13 | 11 | 9 | 10 |
The table shows the distribution of outcomes when a die is thrown 50 times. Calculate the :
(a) Mean deviation of the distribution ; (b) probability that a score selected at random is at least a 4.
(a) Solve : \((x – 2)(x – 3) = 12\).
(b) 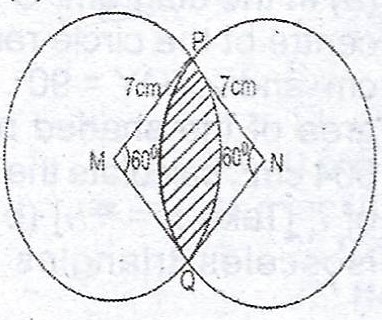 In the diagram, M and N are the centres of two circles of equal radii 7cm. The circle intercept at P and Q. If < PMQ = < PNQ = 60°, calculate, correct to the nearest whole number, the area of the shaded portion. [Take \(\pi = \frac{22}{7}\)].
In the diagram, M and N are the centres of two circles of equal radii 7cm. The circle intercept at P and Q. If < PMQ = < PNQ = 60°, calculate, correct to the nearest whole number, the area of the shaded portion. [Take \(\pi = \frac{22}{7}\)].
(a) 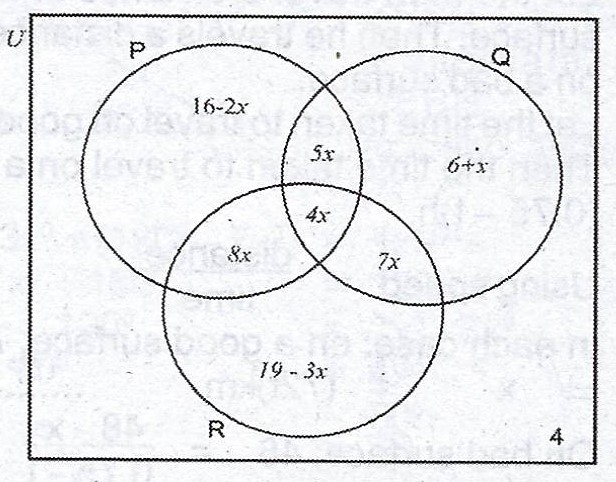
In the Venn diagram, P, Qand R are subsets of the universal set U. If n(U) = 125, find : (i) the value of x ; (ii) n(\(P \cup Q \cap R’\)).
(b) 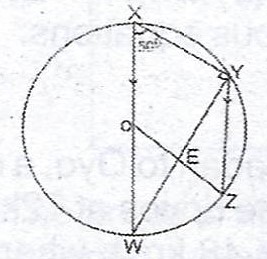 In the diagram, O is the centre of the circle. If WX is parallel to YZ and < WXY = 50°, find the value of (i) , WYZ
In the diagram, O is the centre of the circle. If WX is parallel to YZ and < WXY = 50°, find the value of (i) , WYZ
(ii) < YEZ.
(a) Copy and complete the following table for multiplication modulo 11.
| \(\otimes\) | 1 | 5 | 9 | 10 |
| 1 | 1 | 5 | 9 | 10 |
| 5 | 5 | |||
| 9 | 9 | |||
| 10 | 10 |
Use the table to : (i) evaluate \((9 \otimes 5) \otimes (10 \otimes 10)\);
(ii) find the truth set of :(1) \(10 \otimes m = 2\); (2) \(n \otimes n = 4\)
(b) When a fraction is reduced to its lowest term, it is equal to \(\frac{3}{4}\). The numerator of the fraction when doubled would be 34 greater than the denominator. Find the fraction.
(a) Copy and complete the table of values for the relation \(y = 2 \sin x + 1\)
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° | 240° |
270° |
| y | 1.0 | 2.7 | 0.0 | -0.7 |
(b) Using scales of 2 cm to 30° on the x- axis and 2 cm to 1 unit on the y- axis, draw the graph of \(y = 2 \sin x + 1, 0° \leq x \leq 270°\).
(c) Use the graph to find the values of x for which \(\sin x = \frac{1}{4}\).
(a) If \(\frac{3}{2p – \frac{1}{2}} = \frac{\frac{1}{3}}{\frac{1}{4}p + 1}\), find p.
(b) A television set was marked for sale at GH¢ 760.00 in order to make a profit of 20%. The television set was actually sold at a discount of 5%. Calculate, correct to 2 significant figures, the actual percentage profit.
A building contractor tendered for two independent contracts, X and Y. The probabilities that he will win contract X is 0.5 and not win contract Y is 0.3, What is the probability that he will win :
(a) both contracts ;
(b) exactly one of the contracts ;
(c) neither of the contracts?
(a) 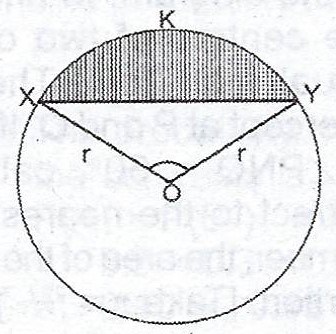
In the diagram, O is the centre of the circle radius r cm and < XOY = 90°.If the area of the shaded part is 504\(cm^{2}\), calculate the value of r. [Take \(\pi = \frac{22}{7}\)].
(b) Two isosceles triangles PQR and PQS are drawn on opposite sides of a common base PQ. If \(< PQR = 66°\) and \(< PSQ = 109°\), calculate the value of \(< RQS\).
(a) Solve the simultaneous equation : \(\frac{1}{x} + \frac{1}{y} = 5 ; \frac{1}{y} – \frac{1}{x} = 1\).
(b) A man drives from Ibadan to Oyo, a distance of 48km in 45 minutes. If he drives at 72 km/h where the surface is good and 48 km/h where it is bad, find the number of kilometers of good surface.
(a) Simplify : \(3\sqrt{75} – \sqrt{12} + \sqrt{108}\), leaving the answer in surd form (radicals).
(b) If \(124_{n} = 232_{five}\), find n.
(a) Without using tables or calculator, simplify : \(\frac{0.6 \times 32 \times 0.004}{1.2 \times 0.008 \times 0.16}\), leaving the answer in standard form (scientific notation).
(b) 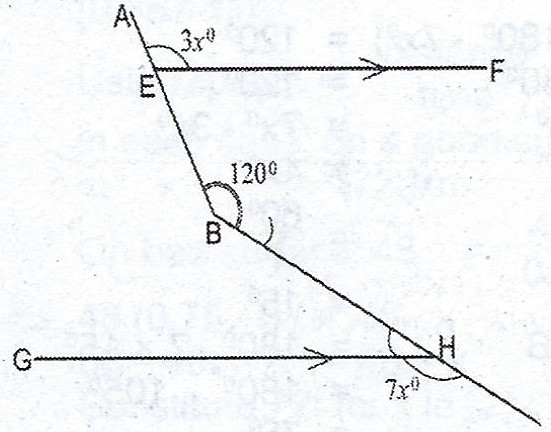
In the diagram, \(\overline{EF}\) is parallel to \(\overline{GH}\). If \(< AEF = 3x°, < ABC = 120°\) and \(< CHG = 7x°\), find the value of \(< GHB\).
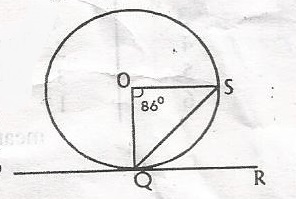
In the diagram, O is the centre of the circle of the circle, PR is a tangent to the circle at Q < SOQ = 86o. Calculate the value of < SQR.
- A. 43o
- B. 47o
- C. 54o
- D. 86o
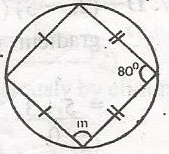
Determine the value of m in the diagram
- A. 80o
- B. 90o
- C. 110o
- D. 150o
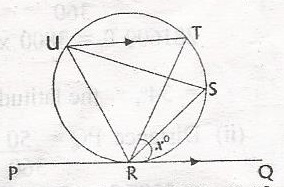
In the figures, PQ is a tangent to the circle at R and UT is parallel to PQ. if < TRQ = xo, find < URT in terms of x
- A. 2xo
- B. (90 - x)o
- C. (90 + x)o
- D. (180 - 2x)o
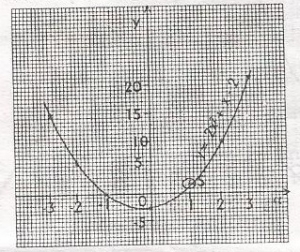
The graph given is for the relation y = 2x2 + x – 1. Find the minimum value of y
- A. 0.00
- B. -0.65
- C. -1.25
- D. -2.10
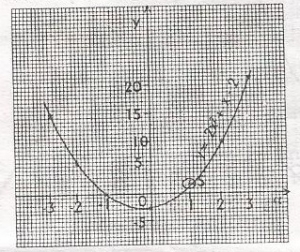
The graph given is for the relation y = 2x\(^2\) + x – 1. What are the coordinates of the point S?
- A. (1, 0.2)
- B. (1, 0.4)
- C. (1, 2.0)
- D. (1, 40)
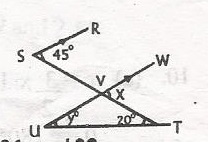
In the diagram, ST is parallel to UW, < WVT = xo, < VUT = yo, < RSV = 45o and < VTU = 20o. Calculate the value of y
- A. 20
- B. 25
- C. 45
- D. 65
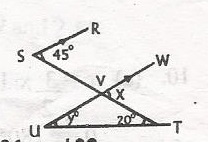
In the diagram, ST is parallel to UW, < WVT = xo, < VUT = yo, < RSV = 45o and < VTU = 20o. Find the value of x
- A. 20
- B. 45
- C. 65
- D. 135
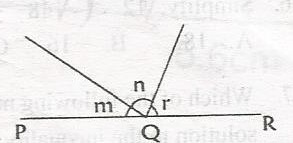
In the diagram, PQR is a straight line, (m + n) = 120o and (n + r) = 100o. Find (m + r)
- A. 110o
- B. 120o
- C. 140o
- D. 160o


