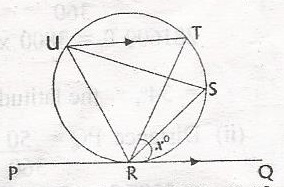
In the figures, PQ is a tangent to the circle at R and UT is parallel to PQ. if < TRQ = xo, find < URT in terms of x
- 2xo
- (90 - x)o
- (90 + x)o
-
(180 - 2x)o
The correct answer is: D
Explanation
< URT = < TRQ (angle alternate a tangent and a chord equal to angle in the alternate segment)< RUT = xo
In \(\bigtriangleup\) URT
< RUT + < RUT + < UTR = 180o (sum of int. < s of \(\bigtriangleup\))
< URT + x + x = 180o
< URT = 180o - 2x