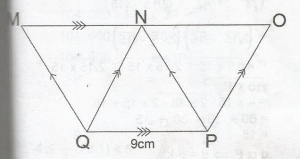
The diagram, MOPQ is a trapezium with QP||MO, MQ||NP, NQ||OP, |QP| = 9cm and the height of \(\Delta\) QNP = 6cm, calculate the area of the trapezium.
- 96cm2
- 90cm2
-
81cm2
- 27cm2
The correct answer is: C
Explanation
Area of \(\Delta\) QNP = \(\frac{1}{2} \times 9 \times 6 \) = 27cm2Area of \(\Delta\) QMN = Area of \(\Delta\) QNP
= Area of \(\Delta\) PNO (triangles between the same parallels)
Hence, area of the trapezium
3 x area of \(\Delta\) QNP
= 3 x 27
= 81cm2