(a) 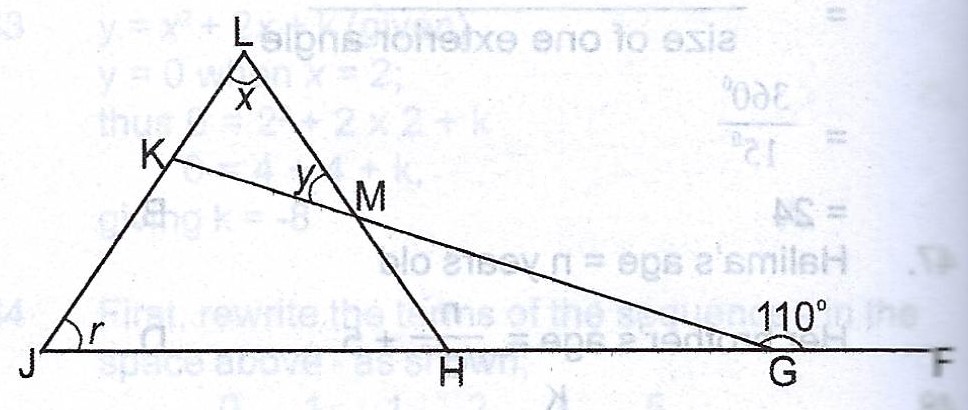
In the diagram, < KLM = x, < LMK = y, < KJH = r and < KGF = 110°. If 2x = r = y, find the value of x.
(b) Ten boys and twelve girls collected donations for a project. The total amount collected by the boys was N600.00 gretaer than that collected by the girls. If the average collection of the boys was N100.00 greater than the average collection of the girls, how much was collected by the two groups?
Explanation
(a) 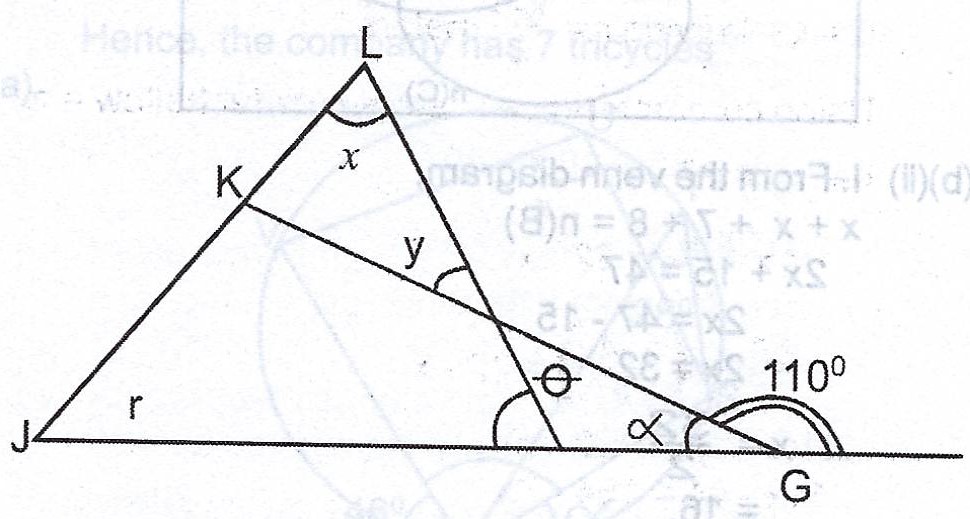
In the diagram above, \(\theta = y\) (vertically opposite angles)
\(\alpha = 180° - 110° = 70°\) (angles on a straight line)
Thus, \(\beta = \theta + \alpha\) (sum of interior opp. angles)
\(\beta = y + 70° ..... (1)\)
\(x + r + \beta = 180° ..... (2)\)
But 2x = r = y
Hence, \(x + 2x + (2x + 70) = 5x + 70 = 180\)
\(5x = 180 - 70 = 110\)
\(x = 22°\)
(b) Let Nx represent the donation collected by the girls. Then, the donation collected by the boys = N(x + 600).
Also, let y represent the average collection, \(x_{g}\), of the girls. Then the average collection, \(x_{b}\), of the boys = N(y + 100).
Thus, \(x_{g} = \frac{x}{12} = y\)
\(x = 12y ... (1)\)
\(x_{b} = \frac{x + 600}{10} = y + 100\)
\(x + 600 = 10(y + 100) .... (2)\)
Substitute 12y for x in (2) :
\(12y + 600 = 10y + 1000\)
\(12y - 10y = 1000 - 600 \)
\(2y = 400 \implies y = 200\)
From (1), \(x = 12y\)
\(\therefore x = 12 \times 200 = N2,400\).
Thus, the girls collected N2,400
The boys collected N2,400 + N600 = N3000
Total = N(2,400 + 3,000) = N5,400

