(a) Copy and complete the table of values, correct to one decimal place, for the relation \(y = 3\sin x + 2\cos x\) for \(0° \leq x \leq 360°\).
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° | 240° | 270° | 300° | 330° | 360° |
| y | 3.0 | 1.6 | -2.0 | -3.6 | -3.0 | 2.0 |
(b) Using scales of 2cm to 30°mon the x- axis and 2cm to 1 unit on the y- axis, draw the graph of the relation \(y = 3\sin x + 2\cos x\) for \(0°\leq x \leq 360°\).
(c) Use the graph to solve :
(i) \(3\sin x + 2\cos x = 0\)
(ii) \(2 + 2\cos x + 3\sin x = 0\).
Explanation
(a)
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° | 240° | 270° | 300° | 330° | 360° |
| y | 2.0 | 3.2 | 3.6 | 3.0 | 1.6 | -0.2 | -2.0 | -3.2 | -3.6 | -3.0 | -1.6 | 0.2 | 2.0 |
(b) 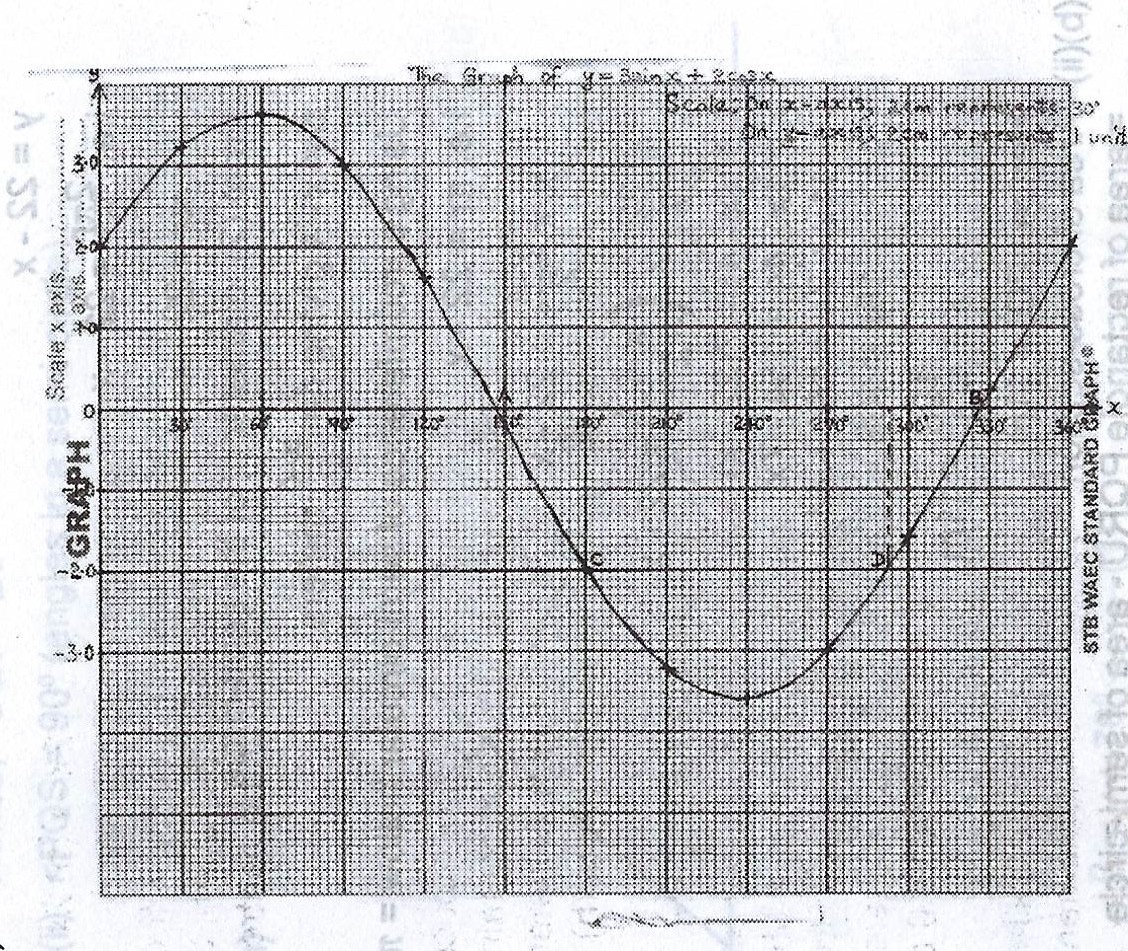
(c)(i) The equation, \(3\sin x + 2\cos x = 0\) has solution where the curve cuts the x- axis, i.e. at A(x = 147°) and B(x = 325.5°).
(ii)First, rearrange \(2 + 2\cos x + 3\sin x = 0\) to have the main graph content \(3\sin x + 2\cos x\) on one side of the equation; i.e. \(3\sin x + 2\cos x = -2\).
Add the line \(y = -2\) to the graph. The line intersects the curve at the points (x = 180°) and (x = 292.5°). Hence, these are the solutions.

