(a) The operation (*) is defined on the set of real numbers, R, by \(x * y = \frac{x + y}{2}, x, y \in R\).
(i) Evaluate \(3 * \frac{2}{5}\).
(ii) If \(8 * y = 8\frac{1}{4}\), find the value of y.
(b) In \(\Delta ABC, \overline{AB} = \begin{pmatrix} -4 \\ 6 \end{pmatrix}\) and \(\overline{AC} = \begin{pmatrix} 3 \\ -8 \end{pmatrix}\). If P is the midpoint of \(\overline{AB}\), express \(\overline{CP}\) as a column vector.
(a) Using completing the square method, solve, correct to 2 decimal places, the equation \(3y^{2} – 5y + 2 = 0\).
(b) Given that \(M = \begin{pmatrix} 1 & 2 \\ 4 & 3 \end{pmatrix}, N = \begin{pmatrix} m & x \\ n & y \end{pmatrix}\) and \(MN = \begin{pmatrix} 2 & 1 \\ 3 & 4 \end{pmatrix}\), find the matrix N.
(a) It takes 8 students two- thirds of an hour to fill 12 tanks with water. How many tanks of water will 4 students fill in one- third of an hour at the same rate?
(b) A chord, 20 cm long, is 12 cm from the centre of the circle. Calculate, correct to one decimal place, the :
(i) angle subtended by the chord at the centre of the circle;
(ii) perimeter of the minor segment cut off by the chord. [Take \(\pi = 3.142\)].
(a) Given that \(\sin x = \frac{5}{13}, 0° < x < 90°\), find \(\frac{\cos x – 2\sin x}{2\tan x}\).
(b) A ladder, LA, leans against a vertical pole at a point L which is 9.6metres above the groung. Another ladder, LB, 12 metres long, leans on the opposite side of the pole and at the same point L. If A and B are 10 metres apart and on the same straight line as the foot of the pole, calculate, correct to 2 significant figures, the :
(i) length of ladder LA (ii) angle which LA makes with the ground.
(a) PQ is a tangent to a circle RST at the point S. PRT is a straight line, < TPS = 34° and < TSQ = 65°.
(i) Illustrate the information in a diagram; (ii) find the value of : (a) < RTS ; (b) < SRP.
(b) 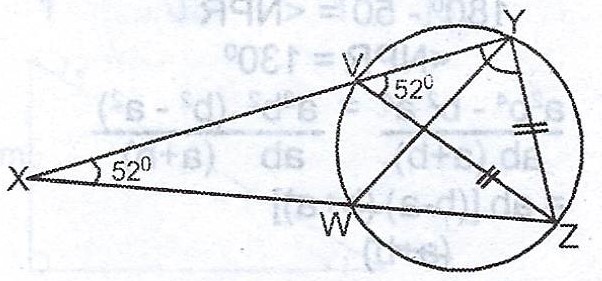
In the diagram, /VZ/ = /YZ/, < YXZ = 20° and < ZVY = 52°. Calculate the size of < WYZ.
| Marks | 1 | 2 | 3 | 4 | 5 |
| Number of students | m + 2 | m – 1 | 2m – 3 | m + 5 | 3m – 4 |
The table shows the distribution of marks scored by some students in a test.
(a) If the mean mark is \(3\frac{6}{23}\), find the value of m.
(b) Find the : (i) interquartile range
(ii) probability of selecting a student who scored at least 4 marks in the test.
(a) Copy and complete the table of values for the equation \(y = 2x^{2} – 7x – 9\) for \(-3 \leq x \leq 6\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 13 | -9 | -14 | -12 | 6 |
(b) Using scales of 2cm to 1 unit on the x- axis and 2cm to 4 units on the y- axis, draw the graphs of \(y = 2x^{2} – 7x – 9\) for \(-3 \leq x \leq 6\).
(c) Use the graph to estimate the :
(i) roots of the equation \(2x^{2} – 7x = 26\);
(ii) coordinates of the minimum point of y;
(iii) range of values for which \(2x^{2} – 7x < 9\).
(a) A manufacturing company requires 3 hours of direct labour to process N87.00 worth of raw materials. If the company uses N30,450.00 worth of raw materials, what amount should it budget at N18.25 per hour?
(b) An investor invested Nx in bank M at the rate of 6% simple interest per annum and Ny in bank N at the rate of 8% simple interest per annum. If a total of N8,000,000.00 was invested in the two banks and the investor received a total of N2,320,000.00 as interest from the two banks after 4 years, calculate the:
(i) values of x and y
(ii) interest paid by the second bank.
Out of 120 customers in a shop, 45 bought both bags and shoes. If all the customers bought either bags or shoes and 11 more customers bought shoes than bags:
(a) Illustrate the this information in a diagram;
(b) find the number of customers who bought shoes;
(c) calculate the probability that a customer selected at random bought bags.
If the sixth term of an Arithmetic Progression (A.P) is 37 and the sum of the first six terms is 147, find the
(a) first term;
(b) sum of the first fifteen terms.
(a) The angle of depression of a point P on the ground from the top T of a building is 23.6°. If the distance from P to the foot of the building is 50m, calculate, correct to the nearest metre, the height if the building.
(b) 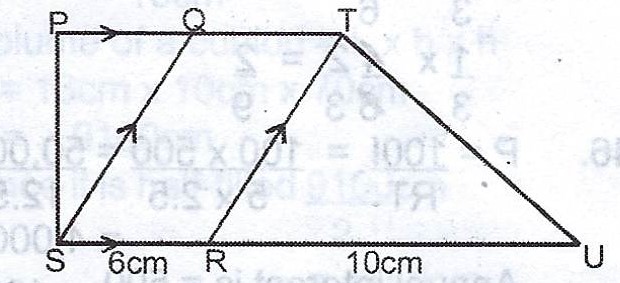
In the diagram, \(PT // SU, QS // TR, /SR/ = 6cm\) and \(/RU/ = 10 cm\). If the area of \(\Delta TRU = 45 cm^{2}\), calculate the area of the trapezium QTUS.
(a) Solve the equation : \(\frac{2}{3}(3x – 5) – \frac{3}{5}(2x – 3) = 3\)
(b) 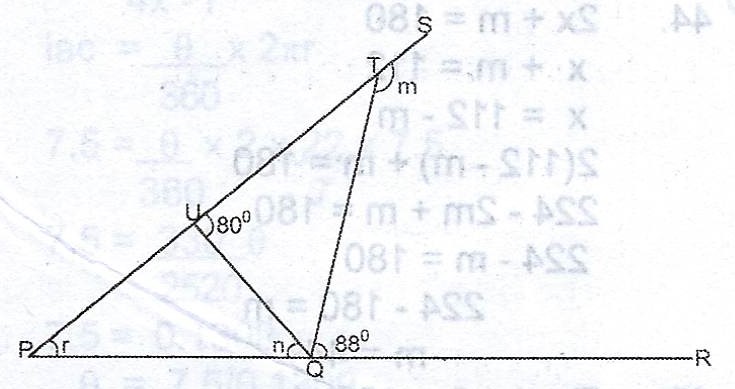
In the diagram, < STQ = m, < TUQ = 80°, < UPQ = r, < PQU = n and < RQT = 88°. Find the value of (m + n).
(a) If \((y – 1)\log_{10}4 = y\log_{10}16\), without using Mathematics tables or calculator, find the value of y.
(b) When I walk from my house at 4km/h, I will get to my office 30mins later than when I walk at 5km/h. Calculate the distance between my house and office.
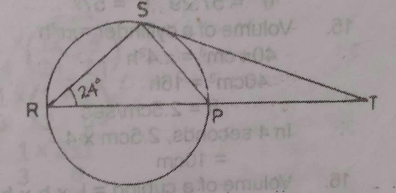
In the diagram, RPS is a diameter of the circle RSP, RP is produced to T and TS is a tangent to the circle at S. If < PRS = 24\(^o\), calculate the value of < STR
- A. 24\(^o\)
- B. 42\(^o\)
- C. 48\(^o\)
- D. 66\(^o\)
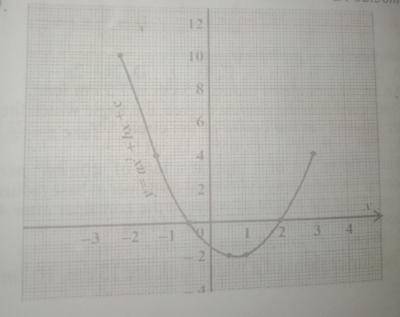
The graph of y = \(ax^2 + bx + c\) is shown oon the diagram. Find the minimum value of y
- A. -2.0
- B. -2.1
- C. -2.3
- D. -2.5
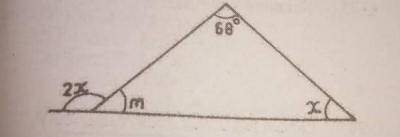
Find the value of m in the diagram
- A. 72\(^o\)
- B. 68\(^o\)
- C. 44\(^o\)
- D. 34\(^o\)
The diagonal of a square is 60 cm. Calculate its peremeter
- A. 20\(\sqrt{2}\)
- B. 40\(\sqrt{2}\)
- C. 90\(\sqrt{2}\)
- D. 120\(\sqrt{2}\)
A stationary boat is observed from a height of 100m. If the horizontal distance between the observer and the boat is 80m, calculate, correct to two decimal places, the angles of depression of the boat from point of observation
- A. 36.87\(^o\)
- B. 39.70\(^o\)
- C. 51.34\(^o\)
- D. 53.13\(^o\)
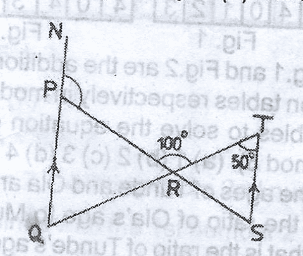
In the diagram, NQ//TS, <RTS = 50\(^o\) and <PRT = 100\(^o\). Find the value of <NPR
- A. 110\(^o\)
- B. 130\(^o\)
- C. 140\(^o\)
- D. 150\(^o\)
In a class of 45 students, 28 offer chemistry and 25 offer Biology. If each student offers at least one of the two subjects, calculate the probability that a student selected at random from the class the class offers chemistry only.
- A. \(\frac{2}{9}\)
- B. \(\frac{4}{9}\)
- C. \(\frac{5}{9}\)
- D. \(\frac{7}{9}\)
| Marks | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 7 | 4 | 18 | 12 | 8 | 11 |
The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, find the first quartile
- A. 1.0
- B. 1.5
- C. 2.0
- D. 2.5


