(a) The angle of depression of a point P on the ground from the top T of a building is 23.6°. If the distance from P to the foot of the building is 50m, calculate, correct to the nearest metre, the height if the building.
(b) 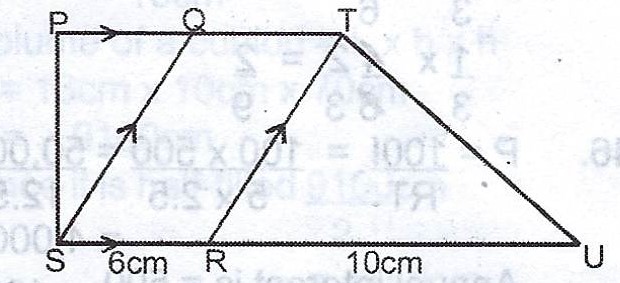
In the diagram, \(PT // SU, QS // TR, /SR/ = 6cm\) and \(/RU/ = 10 cm\). If the area of \(\Delta TRU = 45 cm^{2}\), calculate the area of the trapezium QTUS.
Explanation
(a) 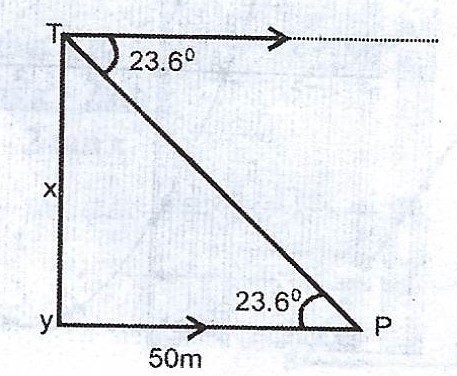
\(< P = 23.6°\) (Alternate angle)
\(\tan 23.6 = \frac{x}{50}\)
\(x = 50\tan 23.6\)
= \(50 \times 0.4369\)
= \(21.845 m \approxeq 22 m\) (to the nearest metre)
(b) Given that \(\Delta TRU = 45cm^{2}\)
\(\implies \frac{1}{2}(bh) = 45\)
\(10h = 45 \times 2 = 90\)
\(h = 9cm\)
Area of trapezium = \(\frac{1}{2}(a + b)h\), where \(a = 6cm; b = 10 + 6 = 16cm; h = 9cm\)
= \(\frac{1}{2}(6 + 16) \times 9\)
= \(11 \times 9\)
= \(99 cm^{2}\)

