Out of 120 customers in a shop, 45 bought both bags and shoes. If all the customers bought either bags or shoes and 11 more customers bought shoes than bags:
(a) Illustrate the this information in a diagram;
(b) find the number of customers who bought shoes;
(c) calculate the probability that a customer selected at random bought bags.
Explanation
(a) 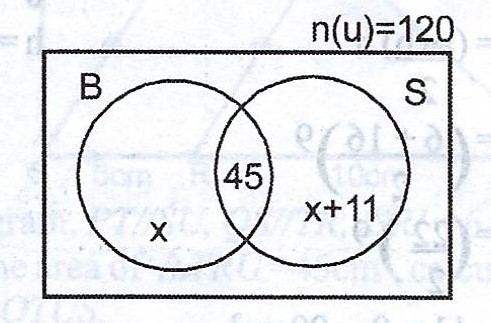
(b) \(x + 45 + x + 11 = 120 \implies 2x + 56 = 120\)
\(2x = 120 - 56 = 64\)
\(x = 32\)
Therefore, the number of customers that bought bags = 32.
(b) the number of customers that bought shoes = 11 + 32 + 45 = 88.
(c) \(P(\text{a random customer bought bags}) = \frac{\text{no of customers that bought bags}}{\text{total no of customers}}\)
No of customers that bought bags = 32 + 45 = 77
\(P(\text{customer bought bag}) = \frac{77}{120}\).

