(a) Copy and complete the table of values for the equation \(y = 2x^{2} – 7x – 9\) for \(-3 \leq x \leq 6\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 13 | -9 | -14 | -12 | 6 |
(b) Using scales of 2cm to 1 unit on the x- axis and 2cm to 4 units on the y- axis, draw the graphs of \(y = 2x^{2} – 7x – 9\) for \(-3 \leq x \leq 6\).
(c) Use the graph to estimate the :
(i) roots of the equation \(2x^{2} – 7x = 26\);
(ii) coordinates of the minimum point of y;
(iii) range of values for which \(2x^{2} – 7x < 9\).
Explanation
(a)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 30 | 13 | 0 | -9 | -14 | -15 | -12 | -5 | 6 | 21 |
(b)
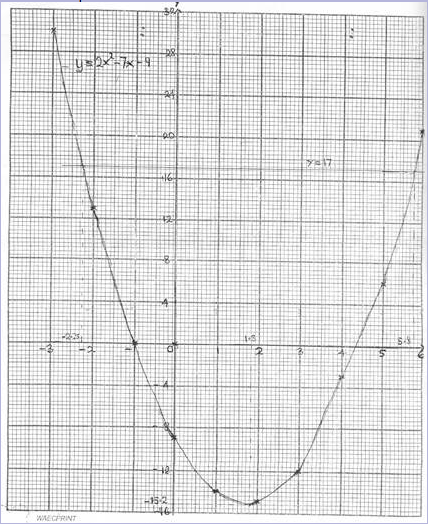
(c) (i) From the graph, the roots of the equation 2x\(^2\) - 7x = 26 can be obtained by drawing a line through y = 17 to meet the curve 2x\(^2\) - 7x - 9.
The roots of the equation 2x\(^2\) - 7x = 26 : -2.2 and 5.8.
(ii) The coordinates of the minimum point of y : 1.8, -15.
(iii) The range of values for which 2x\(^{2}\) - 7x < 9 : - 0.9 < x < 4.5.

