(a) PQ is a tangent to a circle RST at the point S. PRT is a straight line, < TPS = 34° and < TSQ = 65°.
(i) Illustrate the information in a diagram; (ii) find the value of : (a) < RTS ; (b) < SRP.
(b) 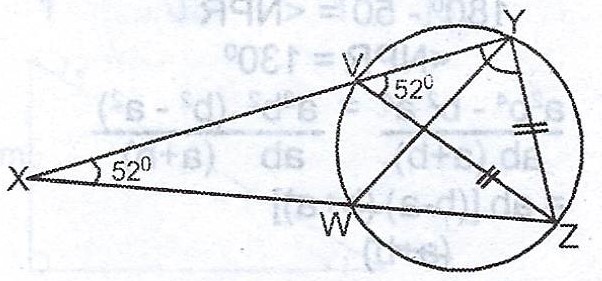
In the diagram, /VZ/ = /YZ/, < YXZ = 20° and < ZVY = 52°. Calculate the size of < WYZ.
Explanation
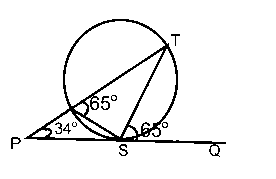
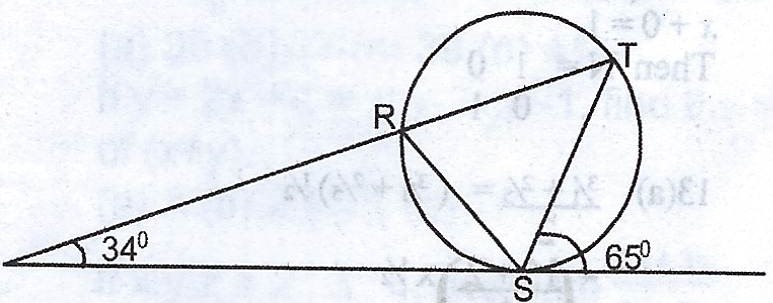
(ii) (a) < RTS = 65° - 34° (exterior angles of triangle PST)
= 31°
(ii) (b) < SRP = 65° (angles in alternate segment are equal)
\(\therefore < SRP = 180° - 65° = 115°\).
(b)
If < XYZ = 128°
then < XZY = 128° + 20° = 148°
< XZV = 180° - 148° = 32°
< YVZ = < VYZ = 52° (Isoceles triangle)
< WYZ = 52° - 32° = 20°

