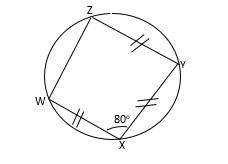
(a) The diagram, = IWYI = IXZI and < WXY = 80\(^o\). What is the size of < XWZ?
(b) A man was charged 2 kobo per month for every N1.00 he borrowed from a bank. At what rate per annum was the interest charged?
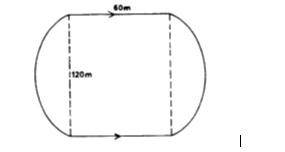
The diagram shows an athletics track with two parallel sides and two semi-circular ends Each of the parallel sides is 60 metres, long and the diameter of each semi-circular end is 120 metres long.
(a) Calculate the distance covered by an athlete who runs round the tack the two times. [Take \(\pi\) = \(\frac{22}{7}\)]
(b) If the athlete spends 200 seconds for the race, calculate the speed in km/h.
Musa is three years older than Manya. Seven years ago, Musa was twice as old as Manya. (1) How old are they now? (2) When will the sum of them be 45?
(a) Evaluate without using calculator, (\(\frac{1}{4} \times 9\frac{1}{7} + \frac{2}{5} (\frac{2}{2} + \frac{3}{4})) \div (\frac{2}{5} – \frac{1}{4})\)
(b) A hunter walked 250 m from point P to Q on a bearing 042\(^o\). Calculate, correct to the nearest meter the vertical distance he has moved.
| Marks | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| Frequency | 1 | 1 | x | 5 | y | 1 | 4 | 3 | 1 |
The frequency distribution shows the marks distribution of a class of 30 students in an examination.
The mean mark of the distribution is 52.
(a) Find the values of x and y.
(b) Construct a group frequency distribution table starting with a lower class limit of 1 and class interval of 10.
(c) Draw a histogram for the distribution
(d) Use the histogram to estimate the mode.
(a) If \(x = \begin{pmatrix} 2 \\ 3 \end{pmatrix}, y = \begin{pmatrix} 5 \\ -2 \end{pmatrix}\) and \(z = \begin{pmatrix} -4 \\ 13 \end{pmatrix}\), find the scalars p and q such that \(px + qy = z\).
(b)(i) Using the scale of 2cm to 2 units on both axis, draw on a graph paper two perpendicular axis x and y for \(-5 \leq x \leq 5, -5 \leq y \leq 5\) respectively.
(ii) Draw, on the graph paper, indicating clearly the vertices and their coordinates,
(1) the quadrilateral WXYZ with W(2, 3), X(4, -1), Y(-3, -4) and Z(-3, 2).
(2) the image \(W_{1}X_{1}Y_{1}Z_{1}\) of the quadrilateral WXYZ under an anti-clockwise rotation of 90° about the origin where \(W \to W_{1}, X \to X_{1}, Y \to Y_{1}\) and \(Z \to Z_{1}\).
(a) Copy and complete the table of values for y = 2x\(^{2}\) + x – 10 for -5 \(\leq\) x \(\leq\) 4.
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | -9 | -10 | 0 |
(b) Using scales of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, Draw the graph of y = 2x\(^{2}\) + x – 10 for -5 \(\leq\) x \(\leq\) 4.
(c) Use the graph to find the solution of :
(i) 2x\(^{2}\) + x = 10
(ii) 2x\(^{2}\) + x – 10 = 2x
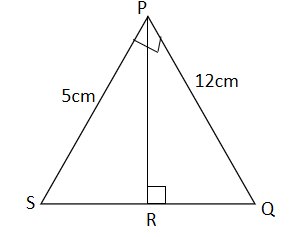
(a) In < PQS, |PQ| = 12 cm, |PS| = 5 cm, < SPQ = < PRQ = 90°, Find, correct to three significant figures, |PR|.
(b) The lengths of two ladders, L and M are 10m and 12m respectively. They are placed against a wall such that each ladder makes angle with the horizontal ground. If the foot of L is 8m from the foot of the wall.
(i) Draw a diagram to illustrate this information; (ii) Calculate the height at which M touches the wall.
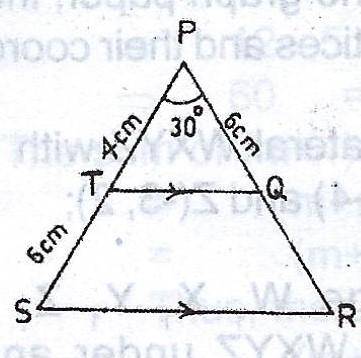
In the diagram, |PT| = 4 cm, |TS| = 6 cm, |PQ| = 6 cm and < SPR = 30°. Calculate, correct to the nearest whole number:
(a) |SR| ;
(b) area of TQRS.
(a) Lamin bought a book for N300.00 and sold it to Bola at a profit of x%. Bola then sold the same book at a profit of x%. If James paid \(N(6x + \frac{3}{4})\) more for the book than Lamin paid, find the value of x.
(b) Find the range of values of x which satisfies the inequality \(3x – 2 < 10 + x < 2 + 5x\).
(a) Find the equation of the line passing through the points (2, 5) and (-4, -7).
(b) Three ships P, Q and R are at sea. The bearing of Q from P is 030° and the bearing of P and R is 300°. If |PQ| = 5 km and |PR| = 8 km,
(i) Illustrate the information in a diagram.
(ii) Calculate, correct to three significant figures, the:
(1) distance between Q and R
(2) bearing of R from Q.
In a road worthiness test on 240 cars, 60% passed. The number that failed had faults in Clutch, Brakes and Steering as follows: Clutch only – 28, Clutch and Steering – 14; Clutch, Steering and Brakes – 8; Clutch and Brakes – 20; Brakes and Steering only – 6. The number of cars with faults in Steering only is twice the number of cars with faults in Brakes only.
(a) Draw a Venn Diagram to illustrate this information.
(b) How many cars had : (i) Faulty Brakes? (ii) Only one fault?
(a) If the mean of m, n, s, p and q is 12, calculate the mean of (m + 4), (n – 3), (s + 6), (p – 2) and (q + 8).
(b) In a community of 500 people, the 75th percentile age is 65 years while the 25th percentile age is 15 years. How many of the people are between 15 and 65 years?
(a) 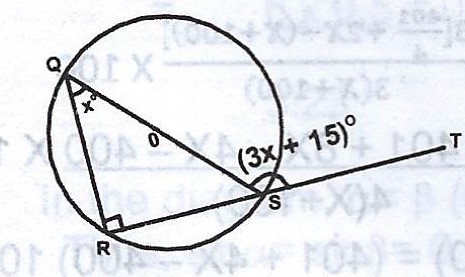
In the diagram
(i) The value of x; (ii)
(b) If \(2N4_{seven} = 15N_{nine}\), find the value of N.
(a) The diagonals of a rhombus are 10.2 cm and 9.3 cm long. Calculate, correct to one decimal place, the perimeter of the rhombus.
(b) Given that \(\sin x = \frac{3}{5}, 0° < x < 90°\), find the value of \(5\cos x – 4\tan x\).
(a) The graph of \(y = 2px^{2} – p^{2}x – 14\) passes through the point (3, 10). Find the values of p.
(b) Two lines, \(3y – 2x = 21\) and \(4y + 5x = 5\) intersect at the point Q. Find the coordinates of Q.
A used car was purchased at N900,000.00. Its value depreciated by 30% in the first year. In each subsequent year, the depreciation was 22% of its value at the beginning of the year. If the car was bought on the 1st of March, 2011, calculate, correct to the nearest hundred naira, the value of the car on the 28th of February, 2015.
The graph of y = x\(^2\) and y = x intersect at which of these points?
- A. (0,0), (1,1)
- B. (0,0), (0,1)
- C. (1, 0), (0, 0)
- D. (0, 0) (0, 0)
M and N are two subsets of the universal set (U). If n(U) = 48, n(M) = 20, n(N) = 30 and n(MUN) = 40, find n(M \(\cap\) N)
- A. 18
- B. 20
- C. 30
- D. 38
The diagonals of a rhombus WXYZ intersect at M. If |MW| = 5cm and |MX| = 12cm, calculate its perimeter
- A. 42cm
- B. 48cm
- C. 52cm
- D. 60cm
Given that Y is 20cm on a bearing of 300\(^o\) from x, how far south of y is x?
- A. 10cm
- B. 15cm
- C. 25cm
- D. 30cm


