(a) The diagonals of a rhombus are 10.2 cm and 9.3 cm long. Calculate, correct to one decimal place, the perimeter of the rhombus.
(b) Given that \(\sin x = \frac{3}{5}, 0° < x < 90°\), find the value of \(5\cos x – 4\tan x\).
Explanation
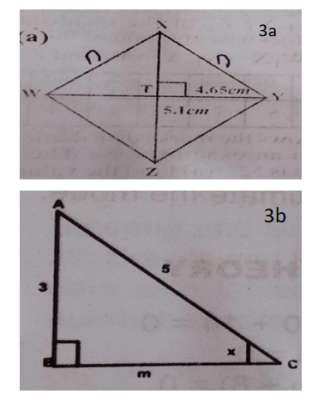
(a) see diagram above
Let a side of the rhombus be n.
Then \(n^{2} = 4.65^{2} + 5.1^{2}\)
= \(21.6225 + 26.01 \)
\(n^{2} = 47.6325\)
\(n = \sqrt{47.6325} = 6.902 cm\)
Hence, the perimeter of the rhombus = 4n
= \(4 \times 6.902\)
= \(27.608 cm \approxeq 27.6 cm\) (to 1 d.p)
(b) Right-angled triangle ABC
see diagram above
\(\sin x = \frac{3}{5}\), Thus, \(m^{2} = 5^{2} - 3^{2} = 25 - 9 = 16\)
\(m = 4\).
\(\cos x = \frac{4}{5} \implies 5\cos x = 5 \times \frac{4}{5} = 4\)
\(\tan x = \frac{3}{4} \implies 4\tan x = 4 \times \frac{3}{4} = 3\)
\(5\cos x - 4\tan x = 4 - 3 = 1\).

