(a) Copy and complete the table of values for y = 2x\(^{2}\) + x – 10 for -5 \(\leq\) x \(\leq\) 4.
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | -9 | -10 | 0 |
(b) Using scales of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, Draw the graph of y = 2x\(^{2}\) + x – 10 for -5 \(\leq\) x \(\leq\) 4.
(c) Use the graph to find the solution of :
(i) 2x\(^{2}\) + x = 10
(ii) 2x\(^{2}\) + x – 10 = 2x
Explanation
(a)
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 35 | 18 | 5 | -4 | -9 | -10 | -7 | 0 | 11 | 26 |
(b) 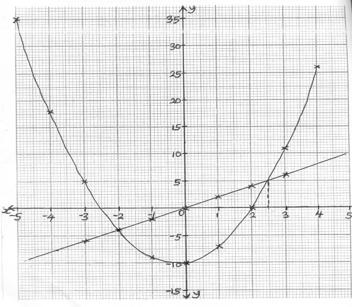
(c)(i) 2x\(^{2}\) + x = 10 \(\equiv\) 2x\(^{2}\) + x - 10 = 0
Thus, the solution of 2x\(^{2}\) + x - 10 = 0 are the values of x at which the curve cuts the x- axis.
x = -2.5 or x = 2.
(ii) 2x\(^{2}\) + x - 10 = 2x
To solve the given equation, we first draw the graph of y = 2x: when x = -2, y = 2(-2) = -4; when x = 3, y = 2(3) = 6.
The values of x at which y = 2x\(^{2}\) + x - 10 and y = 2x intersect give the solution of 2x\(^{2}\) + x - 10 = 2x.
These are x = -2 or x = 2.5.

