(a) Evaluate without using calculator, (\(\frac{1}{4} \times 9\frac{1}{7} + \frac{2}{5} (\frac{2}{2} + \frac{3}{4})) \div (\frac{2}{5} – \frac{1}{4})\)
(b) A hunter walked 250 m from point P to Q on a bearing 042\(^o\). Calculate, correct to the nearest meter the vertical distance he has moved.
Explanation
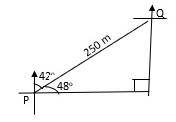
The Chief Examiner reported that in part (a), some Candidates' carried out the requirement of BODMAS correctly tile few couldn't. However, in part (b), most Candidates' could not sketch the diagram correctly and hence failed to earn the marks allocated.
In part (a), expressing as improper fraction we have (\(\frac{1}{4} \times 9\frac{1}{7} + \frac{2}{5} (\frac{2}{2} + \frac{3}{4})) \div (\frac{2}{5} - \frac{1}{4})\) Next, using BODMAS to get (\(\frac{16}{7} + \frac{2}{5} \times \frac{17}{12}) \div \frac{17}{12}\). Simplifying and inverting yields \(\frac{1198}{420} \times \frac{20}{3} = 19\frac{1}{63}\)
In part (b), they were expected to sketch
Then, using trigonometric ratio to have sin 48\(^o\) = \(\frac{x}{250}\) or cos 42\(^o\) = \(\frac{x}{250}\) and simplifying the vertical distance moved to be 186 m.

