
In the diagram, \(\overline{RT}\) and \(\overline{RT}\) are tangent to the circle with centre O. < TUS = 68 °, < SRT = x, and < UTO = y. Find the value of x.
(b) Two tanks A and B am filled to capacity with diesel. Tank A holds 600 litres of diesel more than tank B. If 100 litres of diesel was pumped out of each tank, tank A would then contain 3 times as much diesel as tank B. Find the capacity of each tank.
(a) Given that sin y = \(\frac{8}{17}\) find the value of \(\frac{tan y}{1 + 2 tan y}\)
(b) An amount of N300,000.00 was shared among Otobo, Ada and Adeola. Otobo received N60,000.00, Ada received \(\frac{5}{10}\) of the remainder, while the rest went to Adeola. In what ratio was the money shared?
(a) The third and sixth terms of a Geometric Progression (G.P) are and \(\frac{1}{4}\) and \(\frac{1}{32}\) respectively.
Find:
(i) the first term and the common ratio;
(ii) the seventh term.
(b) Given that 2 and -3 are the roots of the equation ax\(^2\) ± bx + c = 0, find the values of a, b and c.
A woman bought 130 kg of tomatoes for 52,000.00. She sold half of the tomatoes at a profit of 30%. The rest of the tomatoes began to go bad, she then reduced the selling price per kg by 12%. Calculate:
(a) the new selling price per kg;
(ii) the percentage profit on the entire sales if she threw away 5 kg of bad tomatoes.
(a) Copy and complete the table of values for y = 2 cos x + 3 sin x for 0\(^o\) \(\geq\) x \(\geq\) 360\(^o\)
| x | 0\(^o\) | 60\(^0\) | 120\(^o\) | 180\(^o\) | 240\(^o\) | 300\(^o\) | 360\(^o\) |
| y | 2.0 | – 3.6 |
(b) Using a scale of 2cm to 60\(^o\) on the x-axis and 2cm to 1 unit in the y-axis, draw the graph of y = 2 cos x + 3 sin x for 0\(^o\) \(\geq\) 360\(^o\)
(c) Using the graph,
(i) Solve 2 cos x + 3 sin x = -1
(ii) Find, correct to one decimal place, the value of y when x = 342\(^o\)
(a) Solve the inequality \(\frac{1}{3}x – \frac{1}{4} (x + 2) \geq 3x – 1\frac{1}{3}\)
(b)

In the diagram, ABC is right-angled triangle on a horizontal ground. |AD| is a vertical tower. < BAC = 90\(^o\), < ACB = 35\(^o\), < ABD = 52\(^o\) and |BC| = 66cm.
Find, correct to two decimal places:
(I) the height of the tower
(ii) the angle of elevation of the top of the tower from C
The data shows the marks obtained by students in a biology test
| 52 | 56 | 25 | 56 | 68 | 73 | 66 | 64 | 56 | 48 |
| 20 | 39 | 9 | 50 | 46 | 54 | 54 | 40 | 50 | 96 |
| 36 | 44 | 18 | 97 | 65 | 21 | 60 | 44 | 54 | 32 |
| 92 | 49 | 37 | 94 | 72 | 88 | 89 | 35 | 59 | 34 |
| 15 | 88 | 53 | 16 | 84 | 52 | 72 | 46 | 60 | 42 |
(a) Construct a frequency distribution table using the class interval 0 – 9, 10 – 19, 19, 20, 29…
(b) Draw a cumulative frequency curve for the distribution
(c) Use the graph to estimate the;
(i) median
(ii) Percentage of students who scored at least 66 marks, correct to the nearest whole number.
The force of attraction F, between two bodies, varies directly as the product of their masses, \(m_1\) and m\(_2\) and inversely as the square of the distance, d, between them. Given that F = 20N, when m\(_1\) = 25kg, m\(_2\) = 10kg and d = 5m, find:
(I) an expression for F in terms of m\(_1\), m\(_2\) and d;
(ii) the distance, d for F = 30N, m\(_1\) = 7.5kg and m\(_2\) = 4kg
(b) Find the value of x in the diagram

Three red balls, five green balls, and a number of blue balls are put together in a sack. One ball is picked at random from the sack. If the probability of picking a red ball is \(\frac{1}{6}\) find;
(a) The number of blue balls in the sack
(b) the probability of picking a green ball
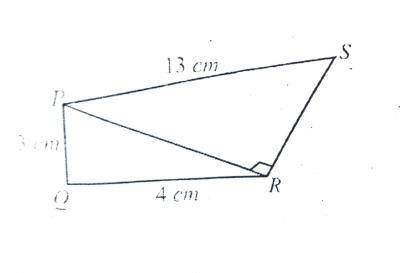
In the diagram, PQRS is a quadrilateral, < PQR = < PRS = 90\(^o\), |PQ| =3cm, |QR| = 4cm and |PS| = 13 cm. Find the area of the quadrilateral.
(a) Ali and Yusif shared N420.000.00 in the ratio 3.,; 5 : 8 respectively. Find the sum of Ali and Yusuf’s shares
(b) Solve: 2(\(\frac{1}{8}\))\(^x\) = 32\(^{x – 1}\).
(a) Find the equation of the line which passes through the points A(-2, 7) and B(2, -3)
(b) Given that \(\frac{5b – a}{8b + 3a} = \frac{1}{5}\) = find, correct to two decimal places, the value \(\frac{a}{b}\)
Evaluate: \(\frac{0.42 \div 2.5}{0.5 \times 2.95}\), leaving the answer in the standard form.
- A. 1.639 x 10\(^2\)
- B. 1.639 x 10\(^1\)
- C. 1.639 x 10\(^{-1}\)
- D. 1.639 x 10\(^{-2}\)
8, 18, 10,14, 18, 11, 13, 14, 13, 17, 15, 8, 16, and 13
The following are scores obtained by some students in a test. How many students scored above the mean score?
- A. 10
- B. 9
- C. 8
- D. 7
The following are scores obtained by some students in a test. Find the median score
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
- A. 14.5
- B. 14.0
- C. 13.5
- D. 13.0
The following are scores obtained by some students in a test, Find the mode of the distribution
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
- A. 18
- B. 14
- C. 13
- D. 8
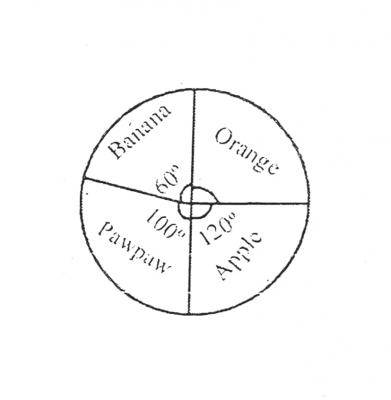
The pie chart represents fruits on display in a grocery shop. If there are 60 oranges on display, how many apples are there?
- A. 90
- B. 80
- C. 70
- D. 40
A box contains 5 red, 6 green and 7 yellow pencils of the same size. What is the probability of picking a green pencil at random?
- A. \(\frac{1}{6}\)
- B. \(\frac{1}{4}\)
- C. \(\frac{1}{3}\)
- D. \(\frac{1}{2}\)
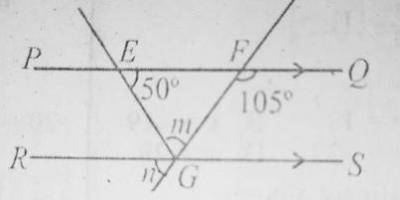
In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of n
- A. 40\(^o\)
- B. 55\(^o\)
- C. 75\(^o\)
- D. 130\(^o\)
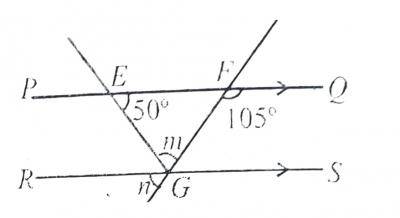
In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of m.
- A. 130\(^o\)
- B. 105\(^o\)
- C. 75\(^o\)
- D. 55\(^o\)
The fourth term of an Arithmetic Progression (A.P) is 37 and the first term is -20. Find the common difference.
- A. 3
- B. 57
- C. 19
- D. 17


