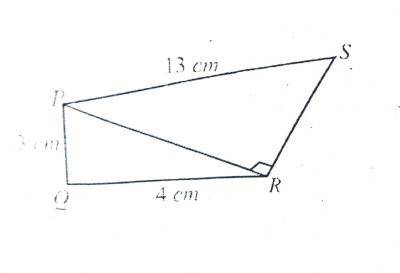
In the diagram, PQRS is a quadrilateral, < PQR = < PRS = 90\(^o\), |PQ| =3cm, |QR| = 4cm and |PS| = 13 cm. Find the area of the quadrilateral.
Explanation
In \(\triangle\)PQR
|PR|\(^2\) = |PQ|\(^2\) + |QR|\(^2\)
= 3\(^2\) + 4\(^2\)
|PR|\(^2\) = 9 + 16
|PR| = \(\sqrt{25}\) = 5cm
In \(\triangle\)PRS
|PS|\(^2\) = |PR|\(^2\) + |RS|\(^2\)
13\(^2\) = 5\(^2\) + |RS|\(^2\)
169 =25 + |RS|\(^2\)
|RS|\(^2\) = 169 - 25
= 144
|RS| = \(\sqrt{144}\) = 12cm
Area of quadrilateral PQRS = Area of \(\triangle\)PQR + Area of \(\triangle\)PQR + Area of \(\triangle\)PRS
= (\(\frac{1}{2} \times 3 \times 4\)) + (\(\frac{1}{2} \times 12 \times 5\))
= 6cm\(^2\) + 30cm\(^2\)
= 36cm\(^2\)

