
(a) In the diagram, AB is a tangent to the circle with centre O, and COB is a straight line. If CD//AB and < ABE = 40°, find: < ODE.
(b) ABCD is a parallelogram in which |\(\overline{CD}\)| = 7 cm, I\(\overline{AD}\)I = 5 cm and < ADC= 125°.
(i) Illustrate the information in a diagram.
(ii) Find, correct to one decimal place, the area of the parallelogram.
(c) If x = \(\frac{1}{2}\)(1 – \(\sqrt{2}\)). Evaluate (2x\(^2\) – 2x).
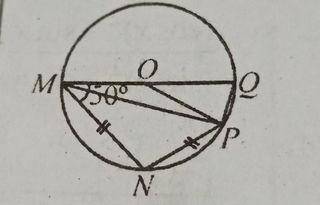
(a) In the diagram, MNPQ is a circle with centre O, |MN| = |NP| and < OMN = 50°. Find:
(I) < MNP
(ii) < POQ
(b) Find the equation of the line which has the same gradient as 8y + 4xy = 24 and passes through the point (-8, 12)
The table shows the distribution of marks obtained by students in an examination.
| Marks (%) | 0 – 9 | 10 – 19 | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 – 69 | 70 – 79 | 80 – 89 | 90 – 99 |
| Frequency | 7 | 11 | 17 | 20 | 29 | 34 | 30 | 25 | 21 | 6 |
(a) Construct a cumulative frequency table for the distribution.
(b) Draw the cumulative frequency curve for the distribution.
(c) Using the curve, find correct to one decimal place, the:
(i) median mark;
(ii) lowest mark for the distinction if 5% of the students passed with distinction
(a) Two cyclists X and Y leave town Q at the same time. Cyclist X travels at the rate of 5 km/h on a bearing of 049° and cyclist Y travels at the rate of 9 km/h on a bearing of 319°.
(a) Illustrate the information on a diagram.
(b) After travelling for two hours, calculate. correct to the nearest whole number, the:
(i) distance between cyclist X and Y;
(ii) bearing of cyclist X from Y.
(c) Find the average speed at which cyclist X will get to Y in 4 hours.
(a) Ms. Maureen spent \(\frac{1}{4}\) of her monthly income at a shopping mall, \(\frac{1}{3}\) at an open market and \(\frac{2}{5}\) of the remaining amount at a Mechanic workshop. If she had N222,000.00 left, find:
(i) her monthly income.
(ii) the amount spent at the open market.
(b) The third term of an Arithmetic Progression (A. P.) is 4m – 2n. If the ninth term of the progression is 2m – 8n. find the common difference in terms of m and n.
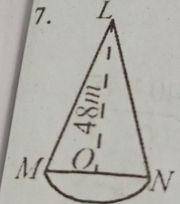
(a) The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 48 m and the base radius is 14. Calculate, correct to three significant figures, the surface area of the structure, [Take \(\pi = \frac{22}{7}\)]
(b) Five years ago, Musah was twice as old as Sesay. If the sum of their ages is 100, find Sesay’s present age.
(a) Copy and complete the table of values for the relation y = 3 sin 2x.
| x | o\(^o\) | 15\(^o\) | 30\(^o\) | 45\(^o\) | 60\(^o\) | 75\(^o\) | 90\(^o\) | 105\(^o\) | 120\(^o\) | 135\(^o\) |
\(^o\) |
| y | 0.0 | 1.5 | -2.6 |
(b) Using a scale of 2 cm to 15° on the x-axis and 2cm to I unit on the y-axis, draw the graph of y = 3 sin 2x for 0° \(\geq\) x \(\geq\) 150°.
(c) Use the graph to find the truth set of;
(i) 3 sin 2x + 2 = 0;
(ii ) \(\frac{3}{2}\) sin 2x = 0.25.
A die was rolled a number of times. The outcomes are as shown in the table
| Number | 1 | 2 | 3 | 4 | 5 | 6 |
| Outcomes | 32 | m | 25 | 40 | 28 | 45 |
If the probability of obtaining 2 is 0.15, find the:
(a) value of m;
(b) number of times the die was rolled;
(c) probability of obtaining an even number.
The total surface area of a cone of slant height 1cm and base radius rcm is 224\(\pi\) cm\(^2\). If r : 1 = 2.5, find:
(a) correct to one decimal place, the value of r
(b) correct to the nearest whole number, the volume of the cone [Take \(\pi\) = \(\frac{22}{7}\)]
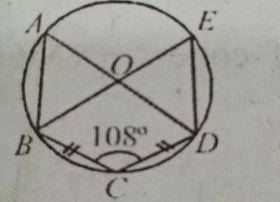
(a} In the diagram, O is the centre of the circle ABCDE, = I\(\overline{BC}\)I = |\(\overline{CD}\)| and < BCD = 108°. Find < CDE.
(b) Given that tan x = \(\sqrt{3}\), 0\(^o\) \(\geq\) x \(\geq\) 90\(^o\), evaluate
\(\frac{(cos x)^2 – sin x}{(sin x)^2 + cos x}\)
(a) Given that P = (\(\frac{rk}{Q} – ms\))\(^{\frac{2}{3}}\)
(i) Make Q the subject of the relation;
(ii) find, correct to two decimal places, the value of Q when P = 3, m = 15, s = 0.2, k = 4 and r = 10.
(b) Given that \(\frac{x + 2y}{5}\) = x – 2y, find x : y
(a) If A = {multiples of 2}, B = {multiples of 3} and C = {factors of 6} are subsets of \(\mu\) = {x:1 \(\leq\) x \(\leq\) 10} find A ′ \(\cap\) B ′ \(\cap\) C′
(b) Tickets for a movie premiere cost $18.50 each while the bulk purchase price for 5 tickets is $80.00. If 4 gentlemen decide to get a fifth person to join them so that they can share the bulk purchase price equally, how much would each person save?
Find the least value of x which satisfies the equation 4x = 7(mod 9)
- A. 7
- B. 6
- C. 5
- D. 4
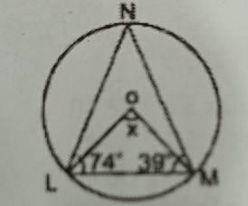
In the diagram, O is the centre of the circle. If < NLM = 74\(^o\), < LMN = 39\(^o\) and < LOM = x, find the value of x.
- A. 134\(^o\)
- B. 126\(^o\)
- C. 113\(^o\)
- D. 106\(^o\)
If (x + 2) is a factor of x\(^2\) +px – 10, find the value of P.
- A. 3
- B. -3
- C. 7
- D. -7
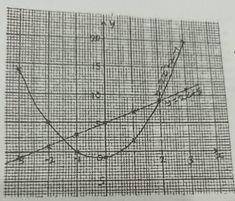
The graph of the equations y = 2x + 5 and y = 2x\(^2\) + x – 1 are shown. Use the information above to answer this question.
If x = -2.5, what is the value of u on the curve?
- A. y = 8.0
- B. y = 8.5
- C. y = 9.0
- D. y = 9.5
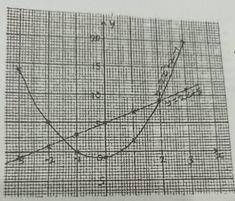
The graph of the equations y = 2x + 5 and y = 2x\(^2\) + x – 1 are shown. Use the information above to answer this question.
Find the point of intersection of the two graphs.
- A. (2.0, 9.0) and (-1.5, 2.0)
- B. (2.0, 8.5) and (-1.5, 2.0)
- C. (2.0, 8.0) and (-1.5, 2.5)
- D. (2.0, 7.5) and (-1.5, 2.5)
The interquartile range of distribution is 7. If the 25th percentile is 16, find the upper quartile.
- A. 35
- B. 30
- C. 23
- D. 9
A woman received a discount of 20% on a piece of cloth she purchased from a shop. If she paid $525.00, what was the original price?
- A. $675.25
- B. $660.25
- C. $656.25
- D. $616.25
Which of the following is not a sufficient condition for two triangles to be congruent?
- A. AAS
- B. SSS
- C. SAS
- D. SSA
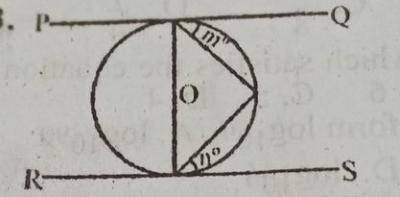
In the diagram, O is the center of the circle. \(\overline{PQ}\) and \(\overline{RS}\) are tangents to the circle. Find the value of (M + N).
- A. 120\(^o\)
- B. 90\(^o\)
- C. 75\(^o\)
- D. 60\(^o\)


