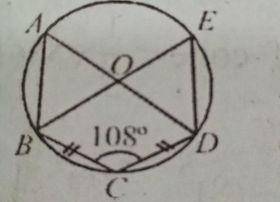
(a} In the diagram, O is the centre of the circle ABCDE, = I\(\overline{BC}\)I = |\(\overline{CD}\)| and < BCD = 108°. Find < CDE.
(b) Given that tan x = \(\sqrt{3}\), 0\(^o\) \(\geq\) x \(\geq\) 90\(^o\), evaluate
\(\frac{(cos x)^2 – sin x}{(sin x)^2 + cos x}\)
Explanation
(a)
C\(B\)D = C\(D\)B = \(\frac{180^o - 107^o}{2}\)
= \(\frac{72^o}{2}\) = 36\(^o\)
< ODE = 90\(^o\) + 36 = 126\(^o\)
(b) tan x = \(\sqrt{3}\)
y\(^2\) (\(\sqrt{3}\))\(^2\) - (l)\(^2\)
y\(^2\) 3 + 1, Cos x = \(\frac{1}{2}\)
y = \(\sqrt{4}\) = 2
sin x = \(\frac{\sqrt{3}}{2}\)
\(\frac{(cos x)^2 - sin x}{(sin x)^2 + cos x}\)
= \(\frac{(\frac{1}{2})^2 - \frac{\sqrt{3}}{2}} {(\frac{\sqrt{3}}{2})^2 + \frac{1}{2}}\)
= \(\frac{\frac{1}{4} - \frac{\sqrt{3}}{2}}{\frac{3}{4} + \frac{1}{2}}\)
= \(\frac{1 - 2\sqrt{3}}{4}\) \(\div\) \(\frac{5}{4}\)
= \(\frac{1 - 2 \sqrt{3}}{4}\) x \(\frac{4}{5}\)
= \(\frac{1 - 2\sqrt{3}}{5}\)

