(a) Copy and complete the table of values for the relation y = 3 sin 2x.
| x | o\(^o\) | 15\(^o\) | 30\(^o\) | 45\(^o\) | 60\(^o\) | 75\(^o\) | 90\(^o\) | 105\(^o\) | 120\(^o\) | 135\(^o\) |
\(^o\) |
| y | 0.0 | 1.5 | -2.6 |
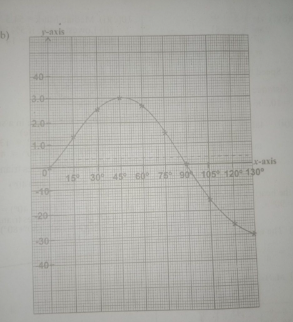
(b) Using a scale of 2 cm to 15° on the x-axis and 2cm to I unit on the y-axis, draw the graph of y = 3 sin 2x for 0° \(\geq\) x \(\geq\) 150°.
(c) Use the graph to find the truth set of;
(i) 3 sin 2x + 2 = 0;
(ii ) \(\frac{3}{2}\) sin 2x = 0.25.
Explanation
| x | o\(^o\) | 15\(^o\) | 30\(^o\) | 45\(^o\) | 60\(^o\) | 75\(^o\) | 90\(^o\) | 105\(^o\) | 120\(^o\) | 135\(^o\) |
\(^o\) |
| y | 0.0 | 1.5 | 2.6 | 2.1 | 2.6 | 1.5 | 0 | - 1.5 | - 2.6 | - 3 | -2.6 |
y = 35m\(^2\)x
when x = 15\(^o\)
y = 3 sin = (15\(^o\))
y = sin 30\(^o\)
y = 3 x \(\frac{1}{2}\) = 1.5
When x = 30\(^o\)
y = 3 sin 2(30\(^o\))
y = 3 sin 60\(^o\) = 2.6
When x = 45\(^o\)
y = 3sin45\(^o\)
= 2.1
When x = 60\(^o\)
y = 3 sin 2(60\(^o\))
= 2 sin 120\(^o\)
= 2.6
When x = 75\(^o\)
y = 3 sin 2(75\(^o\))
= 3 sin 150\(^o\)
= 1.5
When x = 90\(^o\)
y = 3 sin 2(90\(^o\))
= 3 sin 180\(^o\)
= 0
When x = 105\(^o\)
y = 3 sin 2(105\(^o\))
= sin 210\(^o\)
= -1.5
When x = 120\(^o\)
y = 3 sin 2(120\(^o\))
= 3 sin 240\(^o\)
= -2.6
When x = 135\(^o\)
y = 3 sin 2(135\(^o\))
y = 3 sin 270\(^o\)
y = -3
(b
SEE THE GRAPH ABOVE...
(c)(i) 113
(ii) 3\(^o\) and 82\(^o\)

