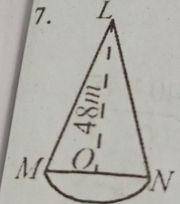
(a) The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 48 m and the base radius is 14. Calculate, correct to three significant figures, the surface area of the structure, [Take \(\pi = \frac{22}{7}\)]
(b) Five years ago, Musah was twice as old as Sesay. If the sum of their ages is 100, find Sesay’s present age.
Explanation
Surface Area of the structure = curved surface area of cone + surface area of hemisphere = \(\pi rl + 2 \pi r^2\)
But slant height l = l\(^2\) = 48\(^2\) + 14\(^2\)
l\(^2\) = 2500
l = \(\sqrt{2500}\) = 50
Surface Area of the structure = \(\pi rl + 2 \pi r^2\) = \(\frac{22}{7}\) x 14 x 50 + 2 x \(\frac{22}{7}\) x 14 x 14
= 3432.0m\(^2\) ≈ 3430m\(^2\) to 3 s.f
(b) Let Musah age be M
Let Sesay be S
M - 5 = 2(S - 5) ......(i)
M + S = 100 ......(ii)
From eqn ii) M = 100 - S
By substitution, 100 - S - 5 = 2(S - 5)
95 - S = 2S - 10
3S = 105
\(\frac{3S}{3} = \frac{105}{3}\)
S = 35
Therefore, Sesay's present age is 35 years

