(a) Two cyclists X and Y leave town Q at the same time. Cyclist X travels at the rate of 5 km/h on a bearing of 049° and cyclist Y travels at the rate of 9 km/h on a bearing of 319°.
(a) Illustrate the information on a diagram.
(b) After travelling for two hours, calculate. correct to the nearest whole number, the:
(i) distance between cyclist X and Y;
(ii) bearing of cyclist X from Y.
(c) Find the average speed at which cyclist X will get to Y in 4 hours.
Explanation
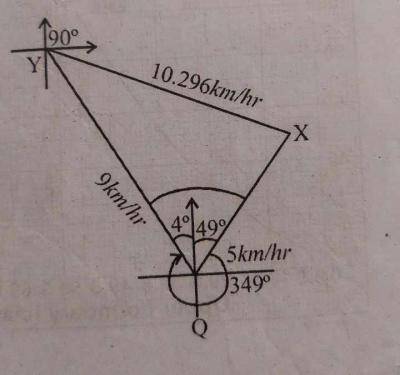
(a) diagram above
(b)(i) m\(^2\) = 5\(^2\) + 9\(^2\)
m\(^2\) = 25 + 81
m\(^2\) = 106
m = \(\sqrt{106}\) = 10.296 km/hr
Speed = \(\frac{distance}{times}\)
distance = speed x time
= 10.296 x 2
= 21km
(b)(ii)
tan\(\theta\) = \(\frac{9km/hr}{5km/hr}\)
tan\(\theta\) = 1.8
\(\theta\) = tan\(^{-1}\)
\(\theta\) = 60.9\(^o\)
the bearing of cyclist x from y
90\(^o\) + 19.9\(^o\) = 109.9\(^o\)
= 110\(^o\)
(c) The average speed = \(\frac{distance }{time}\)
= \(\frac{21}{4}\)km
= 5km/her

