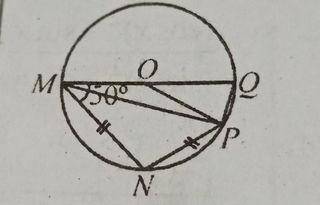
(a) In the diagram, MNPQ is a circle with centre O, |MN| = |NP| and < OMN = 50°. Find:
(I) < MNP
(ii) < POQ
(b) Find the equation of the line which has the same gradient as 8y + 4xy = 24 and passes through the point (-8, 12)
Explanation
(a)

(i)
< NPQ = 180\(^o\) - 50\(^o\) = 130\(^o\)
< MNP = 130\(^o\) - 90\(^o\) = 40\(^o\)
< NMP = 40\(^o\) (Isolceles triangle)
< MNP = 180\(^o\) - (40\(^o\) + 40\(^o\))
= 180\(^o\) - 80\(^o\) = 100\(^o\)
(ii) < OPQ = 90\(^o\)(50\(^o\) - 40\(^o\)) = 80\(^o\)
< OPQ = 80\(^o\) (Isoseles triangle)
< POQ = 180\(^o\) (80\(^o\) + 80\(^o\))
180\(^o\) - 160\(^o\) = 20\(^o\)
(b) 8y + 4x = 24
\(\frac{8y}{8} = \frac{-4y}{8} + \frac{24}{8}\)
y = \(\frac{-1}{2}x + 6\)
m = \(\frac{-1}{2}\)
The equation will give
\(\frac{y - 12}{x + 8} = \frac{-1}{2}\)
2y - 24 = x - 8
2y = - x - 8 + 24
2y = -x + 16

