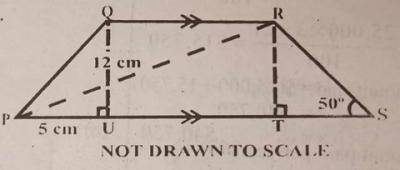
In the diagram, \(\overline{PQ//RS}\) is a trapezium with QR//PS. U and T are points on \(\overline{PS}\) such that \(\overline{|PU|}\) = 5 cm,
\(\overline{|QU|}\) = 12 cm and ∠PUQ= ∠STR =90°. If the area of PQR = 20 cm\(^2\),
calculate, correct to the nearest whole number, the:
(a) perimeter; (b) area; of the trapezium
Explanation
(a) Area of △PQR = \(\frac{1}{2}\) * b * 12 = 20
b = \(\frac{2 x 20}{12}\) = 3.33cm
|QR| = |UT| = 3.33cm
IPQ| = √(12\(^2\) + 5\(^2\))\(^2\) = 13cm
IRT| = |QU| = 12cm
From △RTS
sin 50°= \(\frac{12}{|RS|}\)
|RS| = \(\frac{12}{sin 50°}\) = 15.6649 cm
|TS| = \(\frac{12}{tan 50°}\) = 10.069cm
Perimeter = 13 + 3.33 + 15.6649 + 18.399
= 50.3939cm = 50cm (nearest whole number)
(b)Area= \(\frac{1}{2}\) (3.33+ 18.4004)12
6 (21.7304) = 130.3824cm\(^2\)
= 130 cm\(^2\) (nearest whole number)

