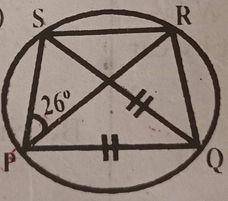
In the diagram, PQRS is a circle. \(\overline{|PQ|}\) = \(\overline{|QS|}\). ∠SPR = 26° and the interior angles of PQS are in the ratio 2:3 :3.
Calculate: (i) PQR; (ii) RPQ; (iii) PRQ
(b) The coordinates of two points P and Q in a plane are (7, 3) and (5, x) respectively, where X is a real number.
If |PQ| = 29units, find the value of x.
Explanation
(a)(i) ∠PSQ = ∠QPS
∠PQS = \(\frac{2}{8}\) x 180°
=45°
∠SPQ = ∠PSQ
= \(\frac{3}{8}\) x 180 = 67.5°
∠SQR = ∠SPR= 26°
∠PQR = ∠PQS + ∠SQR
= 45°+ 26°
= 71°
(ii) ∠RPQ = ∠SPQ - ∠SPR
= 67.5°- 26°
= 41.5°
(iii) ∠PRQ = 180° - 41.5° - 71°
= 67.5°
(b) |PQ| = \(\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2}\)
29 = \(\sqrt{ (5 - 7)^2 + (x - 3)^2}\)
Take the square of both sides
\(29^2\) = \(-2)^2 + (x - 3)^2
841 = 4 + x\(^2\) - 6x + 9
841 = x\(^2\) - 6x + 13
0 = x\(^2\) - 6x + 13 - 841
x\(^2\) - 6x - 828 = 0
Using the formula method
where a = 1, b = -6, and c = -828
x = 31.93095 or - 25.93095
Therefore x ≈ 31. 93 or x = - 25.93

