A chord subtends an angle of 72º at the centre of a circle of radius 24.5m. Calculate the perimeter of the minor segment. [Take π = \(\frac{22}{7}\)
Explanation
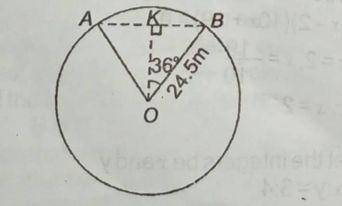
From ΔOKB
sin 36° = \(\frac{|KB|}{24.5}\)
|KB| = 0.5878 x 24.5
=14.4011m
Or
Length of arc = \(\frac{72}{360} * 2 *{\frac{22}{7}} * 24.7\)
=30.8m
Perimeter = 2(14.4011) + 30.8
= 59.6022
= 59.6m

