a) Given that m = tan 30º and n = tan 45º, simplify, without using calculator, \(\frac{ m – n}{mn}\), leaving the answer in the form p + \(\sqrt{q}\)
b) There are 20 women in a bus. 15 of them wear glasses and 10 wear wristwatches. If a woman is chosen at random from the bus, find the probability that she wears both glasses and wristwatches.
Explanation
a) m = tan 60º = \(\frac{\sqrt{3}}{3}\), n = tan 45º = 1
\(\frac{ m - n}{mn}\), = \(\frac{\frac{\sqrt{3}}{3} - 1}{\frac{\sqrt{3}}{3}(1)}\)
= \(\frac{\frac{\sqrt{3} - 3}{3}}{\frac{\sqrt{3}}{3}}\)
= \(\frac{\sqrt{3} - 3}{3}\) X \(\frac{3}{\sqrt{3}}\) = \(\frac{\sqrt{3} - 3}{\sqrt{3}}\)
= \(\frac{\sqrt{3} - 3}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{3 - 3\sqrt{3}}{3}\) = 1 - \(\sqrt{3}\)
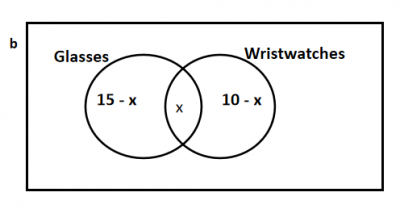
b) see the diagram above..
Let the number of women wearing both wristwatches and glasses be x
15 - x + x + 10 - x = 20
25 - x = 20
x = 5
Therefore, the number of women wearing wrist watches only = 10 - x = 10 - 5 = 5
and number of women wearing glasses only = 15 - x = 15 - 5 = 10
Pr(both) = \(\frac{5}{20}\) = \(\frac{1}{4}\) = 0.25

