The length of the diagonal of a square is 12 cm. Calculate the area of the square.
- A. \(36 cm^2\)
- B. \(48 cm^2\)
- C. \(72 cm^2\)
- D. \(18 cm^2\)
Find the quadratic equation whose roots are \(\frac{2}{3} and \frac{- 3}{4}\)
- A. \(12y^2 - y - 6 = 0\)
- B. \(12y^2 - y + 6 = 0\)
- C. \(12y^2 + y - 6 = 0\)
- D. \(y^2 + y - 6 = 0\)
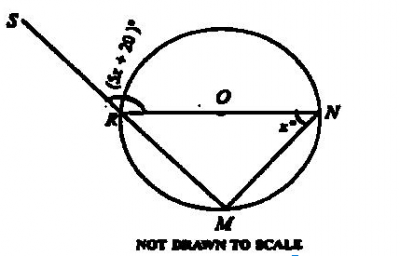
In the diagram, NR is a diameter, ∠MNR = x° and, ∠SRN = (5x + 20)°. Find the value of 2x.
- A. \(42^0\)
- B. \(35^0\)
- C. \(20^0\)
- D. \(90^0\)
The price of a shoe was decreased by 22%. If the new price is $27.3. what is the original price.
- A. $62.30
- B. $42.30
- C. $72.00
- D. $35.00
Write the name of a triangle with the vertices (1, -3), (6, 2) and (0,4)?
- A. Scalene triangle
- B. Isosceles triangle
- C. Right -angle triangle
- D. Equilateral triangle
Consider the statements:
p: Siah is from Foya.
q: Foya is in Lofa.
Write in symbolic for the statement: “If Siah is from Foya, then Foya is in Lofa”
- A. ~q ⇔ p
- B. q ⇒ p
- C. p ⇒ q
- D. p ⇔ q
Mrs Kebeh stands at a distance of 110 m away from a building of vertical height 58 m. If Kebeh is 2 m tall, find the angle of elevation of the top of the building from her eye.
- A. \(27^0\)
- B. \(28^0\)
- C. \(20^0\)
- D. \(26^0\)
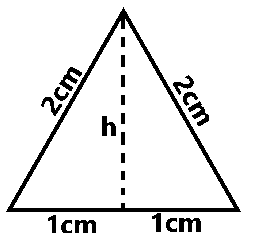
An equilateral triangle has a side 2 cm. Calculate the height of the triangle.
- A. 5cm
- B. \(\sqrt5\)cm
- C. 3cm
- D. \(\sqrt{ 3}\)cm
Factorize completely: \(x^2 – (y + z)^2\)
- A. (x - y - z)(x - y - z)
- B. (x + y + z)(x - y - z)
- C. (x + y + z)(x + y - z)
- D. (x + y - z)(x - y + z)
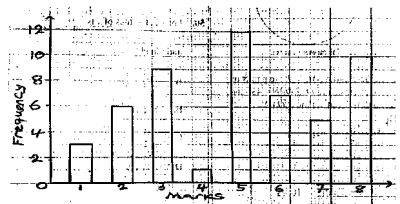
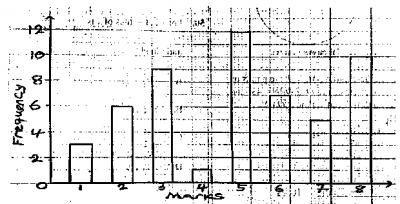
What percentage of the students scored at most 5 marks?
- A. 58.5%
- B. 63.2%
- C. 38.3%
- D. 41.5%
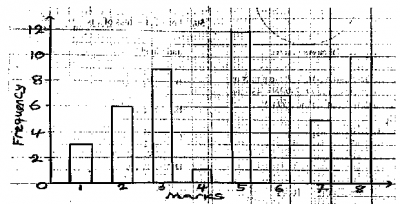
The bar chart represents the distribution of marks scored by students in an economics examination. Use the bar chart to answer questions 30 to 32
If the failed mark was 4, what is the probability that a student selected at random passed?
- A. 0.36
- B. 0.74
- C. 0.52
- D. 0.64
The truth set of \(8 + 2x – x^2\) = 0 is {p, q}. Evaluate p + q.
- A. 4
- B. 2
- C. -6
- D. -2
A bag contains 4 white marbles and 3 blue marbles. Another bag contains 5 red and 6 blue marbles. If a marble is picked at random from each bag, find the probability that they are of the same colour.
- A. \(\frac{9}{11}\)
- B. \(\frac{18}{77}\)
- C. \(\frac{1}{2}\)
- D. \(\frac{11}{12}\)
A line L passing through the point (6, -13) is parallel to the line which passes through (7, 4) and (-3, 9). Find the equation of the line L.
- A. y = \(\frac{1}{2}x - 10\)
- B. y = \(\frac{-1}{2}x + 10\)
- C. y = \(\frac{-1}{2}x - 10\)
- D. y = \(\frac{1}{2}x +10\)
John was facing S35°E. If he turned 90° in the anticlockwise direction, find his new direction.
- A. S55°E.
- B. S35°W.
- C. N55°E.
- D. N35°W.
A number is chosen at random from 40 and 50 inclusive. Find the probability that the number is prime.
- A. \(\frac{8}{11}\)
- B. \(\frac{3}{11}\)
- C. \(\frac{4}{11}\)
- D. \(\frac{5}{11}\)
Arrange the following in ascending order of magnitude \(110_{two}, 31_{eight}, 42_{five}\)
- A. \(110_{two}, 31_{five}, 42_{eight}\)
- B. \(42_{five}, 110_{two}, 31_{eight}\)
- C. \(42_{five}, 31_{eight}, 110_{two}\)
- D. \(110_{two}, 42_{five}, 31_{eight}\)
An empty cylindrical tank is 140 cm in diameter. If 200 litres of water was poured into the tank. Calculate, correct to the nearest centimeter, the height of the water in the tank. (\(Take \pi = \frac{22}{7})\)
- A. 91cm
- B. 7cm
- C. 13cm
- D. 57cm
make x the subject of the relation \(y = \frac{ax^3 – b}{3z}\)
- A. x = \(\sqrt[3] \frac{ax^3 - b}{3z}\)
- B. x = \(\sqrt[3] \frac{3yz - b}{a}\)
- C. x = \(\sqrt[3] \frac{3yz + b}{a}\)
- D. x = \(\sqrt[3] \frac{3yzb}{a}\)